《2022年中考數(shù)學(xué)考前專題輔導(dǎo) 三角函數(shù)復(fù)習(xí)》由會員分享����,可在線閱讀,更多相關(guān)《2022年中考數(shù)學(xué)考前專題輔導(dǎo) 三角函數(shù)復(fù)習(xí)(11頁珍藏版)》請在裝配圖網(wǎng)上搜索���。
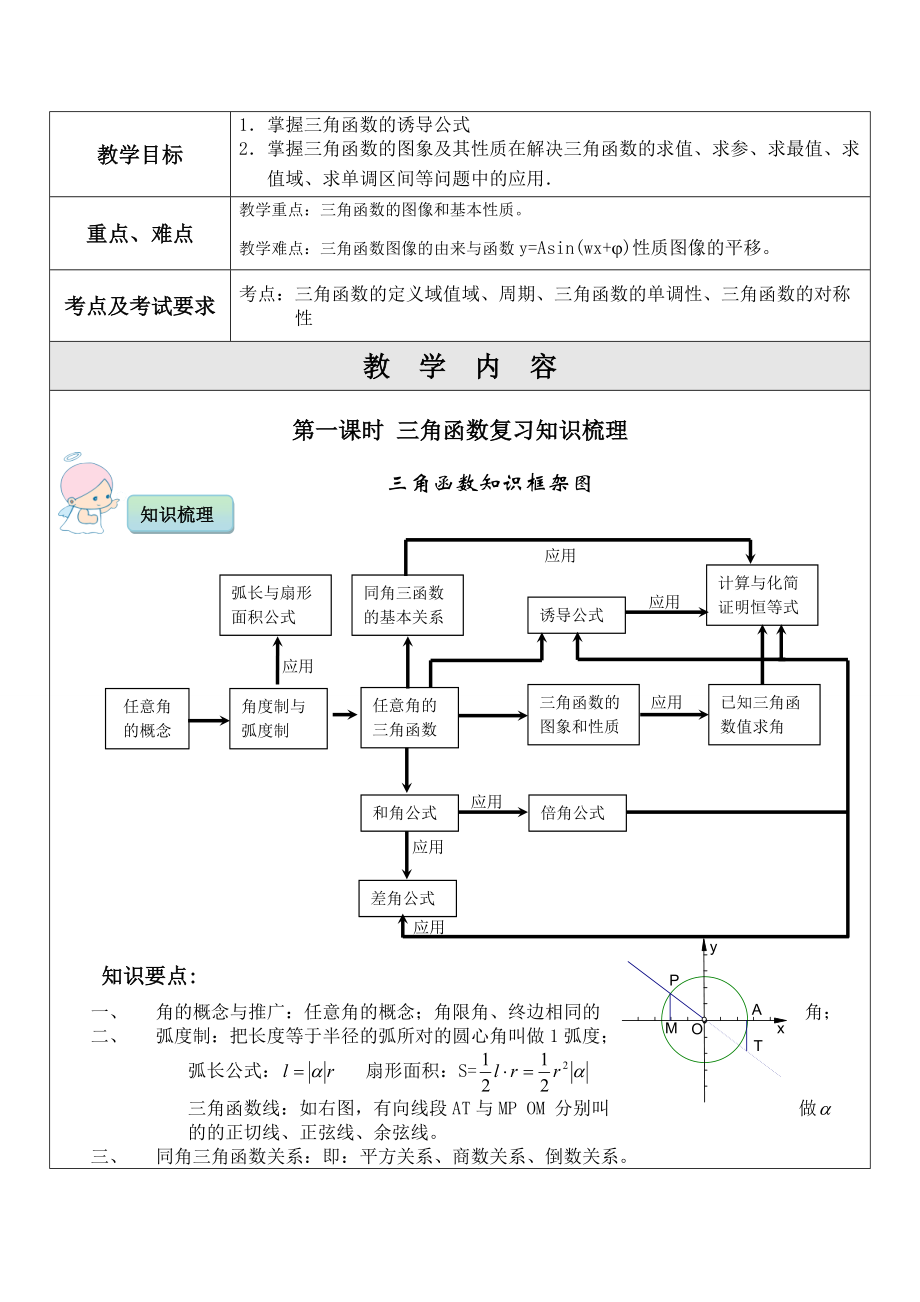
1�、教學(xué)目標(biāo)1掌握三角函數(shù)的誘導(dǎo)公式2掌握三角函數(shù)的圖象及其性質(zhì)在解決三角函數(shù)的求值�����、求參���、求最值���、求 值域����、求單調(diào)區(qū)間等問題中的應(yīng)用重點(diǎn)���、難點(diǎn)教學(xué)重點(diǎn):三角函數(shù)的圖像和基本性質(zhì)���。教學(xué)難點(diǎn):三角函數(shù)圖像的由來與函數(shù)y=Asin(wx+j)性質(zhì)圖像的平移?���?键c(diǎn)及考試要求考點(diǎn):三角函數(shù)的定義域值域、周期����、三角函數(shù)的單調(diào)性、三角函數(shù)的對稱 性教 學(xué) 內(nèi) 容第一課時 三角函數(shù)復(fù)習(xí)知識梳理任意角的概念弧長與扇形面積公式角度制與弧度制同角三函數(shù)的基本關(guān)系任意角的三角函數(shù)誘導(dǎo)公式三角函數(shù)的圖象和性質(zhì)計算與化簡證明恒等式已知三角函數(shù)值求角和角公式倍角公式差角公式應(yīng)用應(yīng)用應(yīng)用應(yīng)用應(yīng)用應(yīng)用應(yīng)用三角函數(shù)知識框架圖知識梳
2��、理知識要點(diǎn):一����、 角的概念與推廣:任意角的概念����;角限角���、終邊相同的角;二��、 弧度制:把長度等于半徑的弧所對的圓心角叫做1弧度�����;弧長公式: 扇形面積:S=三角函數(shù)線:如右圖��,有向線段AT與MP OM 分別叫做的的正切線��、正弦線�����、余弦線�。三、 同角三角函數(shù)關(guān)系:即:平方關(guān)系����、商數(shù)關(guān)系、倒數(shù)關(guān)系���。四�����、 誘導(dǎo)公式: 記憶:單變雙不變����,符號看象限。單雙:即看中的是的單倍還是雙倍����,單倍后面三角函數(shù)名變,雙不變則三角函數(shù)名不變�;符號看象限:即把看成銳角,加上終邊落在第幾象限則是第幾象限角的符號����。五、 有關(guān)三角函數(shù)單調(diào)區(qū)間的確定�、最小正周期、奇偶性��、對稱性以及比較三角函數(shù)值的大小問題,一般先化簡成單角三角函數(shù)
3��、式�����。然后再求解�����。六����、 三角函數(shù)的求值、化簡�����、證明問題常用的方法技巧有:1�����、 常數(shù)代換法:如:2���、 配角方法: 3�、 降次與升次: 以及這些公式的變式應(yīng)用����。4��、 (其中)的應(yīng)用�,注意的符號與象限���。5���、 常見三角不等式:(1)、若 (2)��、若(3)���、6�����、 常用的三角形面積公式:(1)��、 (2)�����、(3)����、七、 三角函圖象和性質(zhì):正弦函數(shù)圖象的變換:三角函數(shù)的圖象和性質(zhì)定義域RR值 域RR周期性奇偶性對稱性奇函數(shù)�,圖象關(guān)于坐標(biāo)原點(diǎn)對稱偶函數(shù)�����,圖象關(guān)于 軸對稱奇函數(shù)���,圖象關(guān)于坐標(biāo)原點(diǎn)對稱奇函數(shù)�����,圖象關(guān)于原點(diǎn)對稱單調(diào)性在區(qū)間 上單調(diào)遞增��;在區(qū)間 上單調(diào)遞減���。在區(qū)間 上單調(diào)遞增;在區(qū)間 上單調(diào)遞減�。在區(qū)間上
4、單調(diào)遞增�。在區(qū)間 上單調(diào)遞減。第二課時 三角函數(shù)復(fù)習(xí)考點(diǎn)分析考點(diǎn)分析考點(diǎn)一: 求三角函數(shù)的定義域���、值域和最值�、三角函數(shù)的性質(zhì)(包括奇偶性、單調(diào)性�����、周期性)這類問題在選擇題�����、填空題��、解答題中出現(xiàn)較多���,主要是考查三角的恒等變換及三角函數(shù)的基礎(chǔ)知識���。例1、已知函數(shù)f(x)=(1) 求它的定義域和值域�����;求它的單調(diào)區(qū)間�����;判斷它的奇偶性;判斷它的周期性��。解題思路分析: (1)x必須滿足sinx-cosx0�,利用單位圓中的三角函數(shù)線及,kZ 函數(shù)定義域?yàn)?,kZ 當(dāng)x時, 函數(shù)值域?yàn)?(3) f(x)定義域在數(shù)軸上對應(yīng)的點(diǎn)關(guān)于原點(diǎn)不對稱 f(x)不具備奇偶性 (4) f(x+2)=f(x) 函數(shù)f(x)最小正
5���、周期為2注;利用單位圓中的三角函數(shù)線可知����,以、象限角平分線為標(biāo)準(zhǔn)����,可區(qū)分sinx-cosx的符號。例2��、化簡并求函數(shù)的值域和最小正周期.解: 所以函數(shù)f(x)的值域?yàn)?�,最小正周期?�、(1)已知cos(2+)+5cos=0,求tan(+)tan的值���; (2)已知�,求的值。解題思路分析:從變換角的差異著手�����。 2+=(+)+��,=(+)- 8cos(+)+5cos(+)-=0展開得: 13cos(+)cos-3sin(+)sin=0同除以cos(+)cos得:tan(+)tan=(1) 以三角函數(shù)結(jié)構(gòu)特點(diǎn)出發(fā) tan=2 例4�����、求函數(shù)y=sin2x+2sinxcosx+3cos2的最大值解:2sin
6�����、xcosx=sin2x,sin2x+cos2x=1,cos2x=y=sin2x+2sinxcosx+3cos2x=(sin2x+cos2x)+2sinxcosx+2cos2x=1+sin2x+2 =sin2x+cos2x+2=(sin2xcos+cos2xsin)+2= sin(2x+)+2當(dāng)2x+=+2k時,ymax=2+ 即x=+K(KZ)���,y的最大值為2+注�����;齊次式是三角函數(shù)式中的基本式���,其處理方法是化切或降冪���。考點(diǎn)二: 三角與其他知識的結(jié)合,三角函數(shù)仍將以選擇題����、填空題和解答題三種題型出現(xiàn),難度會控制在中等偏易的程度���;例5�����、已知00900,且sin����,sin是方程=0的兩個實(shí)數(shù)根,求si
7��、n(-5)的值��。解題思路分析:由韋達(dá)定理得sin+sin=cos400�����,sinsin=cos2400- sin-sin= 又sin+sin=cos400 000,0)��,在一個周期內(nèi)�,當(dāng)x=時,ymax=2�;當(dāng)x=時,ymin=-2���,則此函數(shù)解析式為A����、 B��、C��、 D����、4、已知tan�����,tan是方程兩根��,且,則+等于( )A�����、 B���、或 C�����、或 D���、5、函數(shù)f(x)=3sin(x+100)+5sin(x+700)的最大值是A�、5.5 B、6.5 C�����、7 D��、86.方程sinx=lgx的實(shí)根個數(shù)是( )(A)1 (B)2 (C)3 (D)以上都錯7.在ABC中�����,(1)已知tanA= sinB=���,則C有
8�����、且只有一解����,(2)已知tanA=,sinB=,則C有且只有一解��,其中正確的是( )(A)只有(1) (B)只有(2)(C)(1)與(2)都正確 (D)(1)與(2)均不正確8�、的三內(nèi)角所對邊的長分別為設(shè)向量,若,則角的大小為( )(A) (B) (C) (D) 9、設(shè),點(diǎn)是線段上的一個動點(diǎn),若,則實(shí)數(shù)的取值范圍是( )(A) (B) (C) (D) 10�����、已知,且關(guān)于的方程有實(shí)根,則與的夾角的取值范圍是 ( )A.0, B. C. D.11��、函數(shù)f(x)=sin(x+)+cos(x-)的圖象關(guān)于y軸對稱����,則=_。12�、數(shù)y=2sinxcosx-(cos2x-sin2x)的最大值與最小值的積為_
9����、����。13、知(x-1)2+(y-1)2=1�,則x+y的最大值為_。14�、是否存在實(shí)數(shù)a,使得函數(shù)y=sin2x+acosx+在閉區(qū)間0����,上的最大值是1?若存在��,求出對應(yīng)的a值���。15�、已知f(x)=5sinxcosx-cos2x+(xR)(1) 求f(x)的最小正周期�;求f(x)單調(diào)區(qū)間���;求f(x)圖象的對稱軸����,對稱中心。16�、函數(shù)y=cosx-1(0x2)的圖像與x軸所圍成圖形的面積是_。(考查三角函數(shù)圖形的對稱變換)17�����、設(shè)三角函數(shù)f(x)=sin(+)��,其中k0(1)寫出f(x)的極大值M�,極小值m,最小正周期T��。(2)試求最小的正整數(shù)k���,使得當(dāng)自變量x在任意兩個整數(shù)間(包括整數(shù)本身)變化時�����,函數(shù)f(x)至少有一個值是M與一個值m�����,(考查三角函數(shù)的最值�����、周期��,以及分析問題�����、解決問題的能力)18�、是否存在實(shí)數(shù)a,使得函數(shù)y=sin2x+acosx+在閉區(qū)間0�����,上的最大值是1���?若存在���,求出對應(yīng)的a值。19. (本小題滿分13分)已知A���、B����、C是三內(nèi)角�����,向量且�����,(1)求角A�; (2) 若20、已知�,將的圖象按向量平移后,圖象關(guān)于直線對稱�����。(1)�、求實(shí)數(shù)的值,并求取得最大值時的x的集合�����。(2)���、求的單調(diào)遞增區(qū)間����。
 2022年中考數(shù)學(xué)考前專題輔導(dǎo) 三角函數(shù)復(fù)習(xí)
2022年中考數(shù)學(xué)考前專題輔導(dǎo) 三角函數(shù)復(fù)習(xí)