《高中數(shù)學(xué)《垂直關(guān)系的性質(zhì)》學(xué)案1 北師大版必修2》由會(huì)員分享，可在線(xiàn)閱讀，更多相關(guān)《高中數(shù)學(xué)《垂直關(guān)系的性質(zhì)》學(xué)案1 北師大版必修2（2頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
1、§1 垂直關(guān)系的性質(zhì)（第三課時(shí)）
一、 學(xué)習(xí)目標(biāo)：
1. 掌握直線(xiàn)與平面及平面與平面垂直的性質(zhì)定理，并會(huì)應(yīng)用。
2. 通過(guò)定理的學(xué)習(xí)，培養(yǎng)和發(fā)展學(xué)生的空間想象能力，推理論證能力，運(yùn)用圖形語(yǔ)言進(jìn)行交流的能力，幾何直觀感知能力
二．重點(diǎn)知識(shí)（課前自學(xué)完成）
1.閱讀課本P38-40完成下列問(wèn)題。
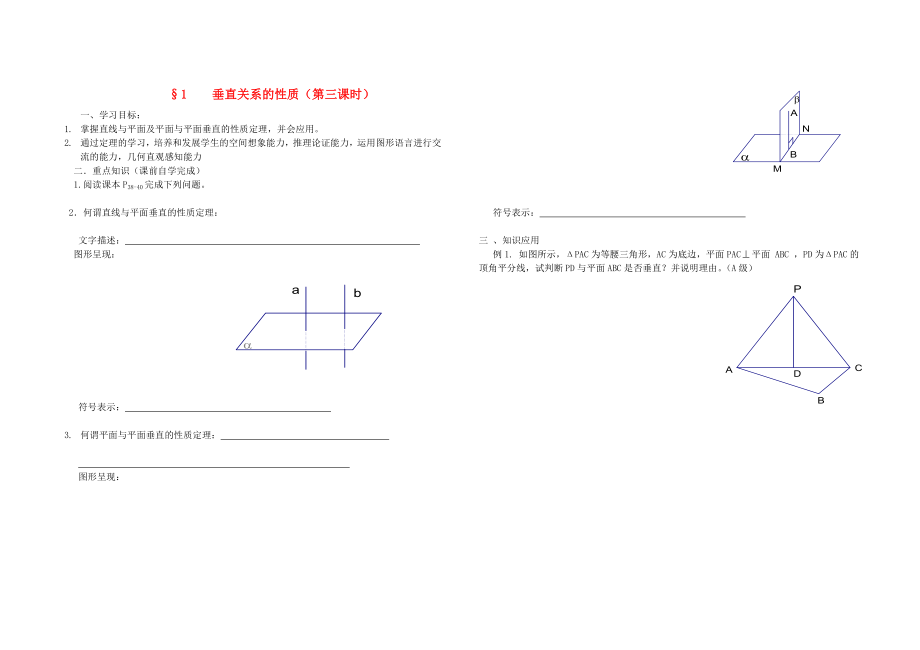
2．何謂直線(xiàn)與平面垂直的性質(zhì)定理：
文字描述：
圖形呈現(xiàn)：
2、
符號(hào)表示：
3. 何謂平面與平面垂直的性質(zhì)定理：
圖形呈現(xiàn)：
符號(hào)表示：
三 、知識(shí)應(yīng)用
例1. 如圖所示，ΔPAC為等腰三角形，AC為底邊，平面PAC平面 ABC ，PD為ΔPAC的
3、頂角平分線(xiàn)，試判斷PD與平面ABC是否垂直？并說(shuō)明理由。（A級(jí)）
例2.如圖所示，在正三棱柱ABC- A1B1C1中，E，M分別為BB1，A1C的中點(diǎn)，求證：
（1）EM平面A A1C1C
（2）平面A1EC平面AA1C1C；（B級(jí)）
四 自測(cè)達(dá)標(biāo)
1.對(duì)于直線(xiàn)m, n和平面，，能得出的一個(gè)條件是（A級(jí)） （ ）
2.下列命題錯(cuò)誤的是 (B級(jí)) （ ）
A．若，那么內(nèi)的所有直線(xiàn)都垂直于
B.
4、 若，那么內(nèi)一定存在直線(xiàn)平行于
C. 若不垂直于，那么內(nèi)一定不存在直線(xiàn)垂直于
D. 若，那么內(nèi)有無(wú)數(shù)條直線(xiàn)都垂直于
3.若直線(xiàn)a//直線(xiàn)b，且a平面，則直線(xiàn)b與平面的關(guān)系是 （填“一定”或“不一定”）垂直（A級(jí)）
4.已知三棱錐P-ABC，PA=PB，AC=BC，D為AB的中點(diǎn)，
（1）求證：平面PAB平面PCD
（2）求證：若E為PCD的垂心，則CE平面PAB（B級(jí)）
5. 有公共底邊的兩個(gè)等腰ABC和等腰BCD，已知AB=AC=13，BD=CD=6，BC=10，試求AD為何值時(shí)，平面BCD平面ABC 。（B級(jí)）
高中數(shù)學(xué)《垂直關(guān)系的性質(zhì)》學(xué)案1 北師大版必修2
