（江蘇專用）高考數(shù)學(xué)專題復(fù)習(xí) 專題10 概率與統(tǒng)計(jì) 第67練 隨機(jī)事件的頻率與概率練習(xí) 文-人教版高三數(shù)學(xué)試題

《（江蘇專用）高考數(shù)學(xué)專題復(fù)習(xí) 專題10 概率與統(tǒng)計(jì) 第67練 隨機(jī)事件的頻率與概率練習(xí) 文-人教版高三數(shù)學(xué)試題》由會(huì)員分享，可在線閱讀，更多相關(guān)《（江蘇專用）高考數(shù)學(xué)專題復(fù)習(xí) 專題10 概率與統(tǒng)計(jì) 第67練 隨機(jī)事件的頻率與概率練習(xí) 文-人教版高三數(shù)學(xué)試題（4頁珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

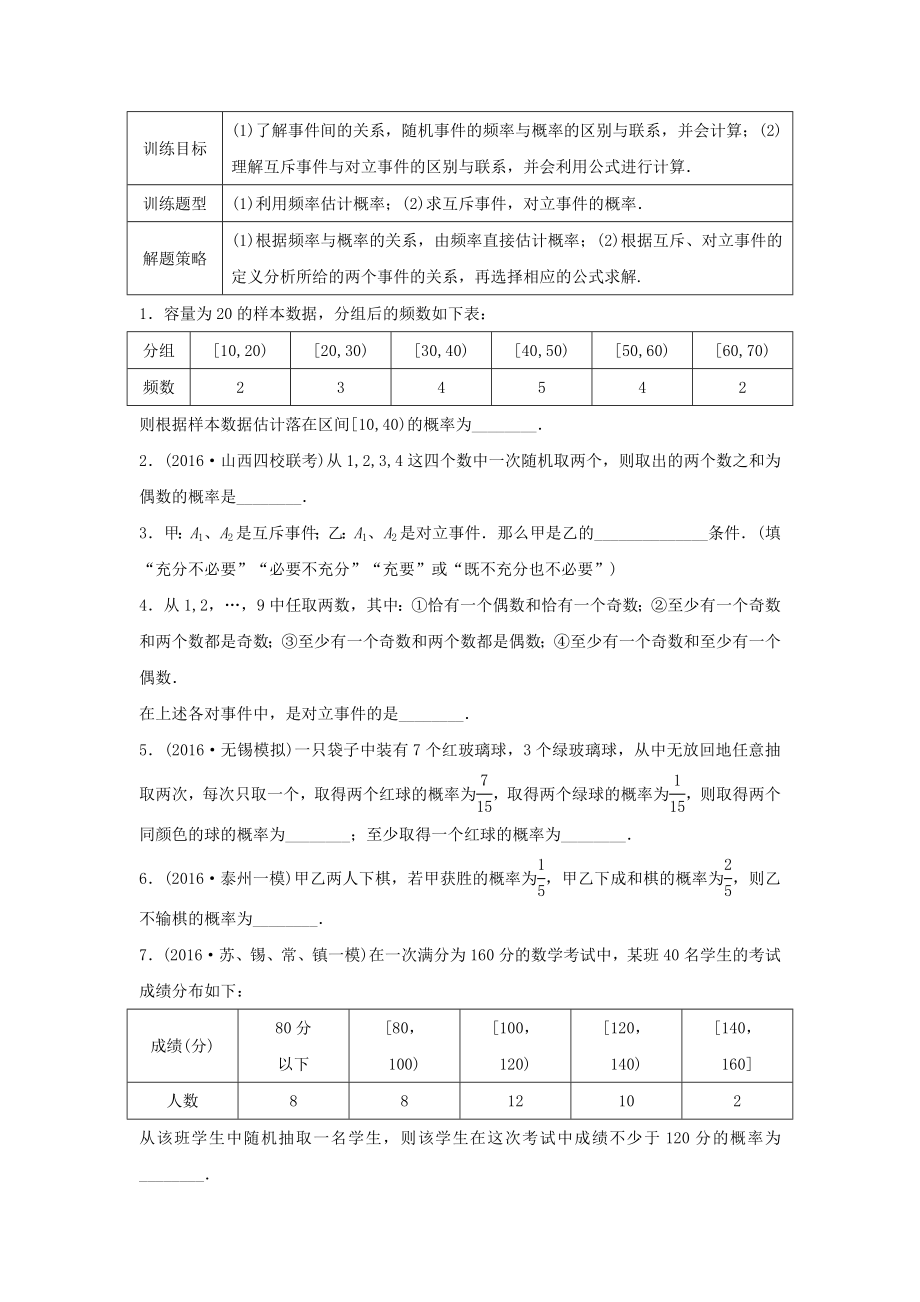
1、訓(xùn)練目標(biāo)(1)了解事件間的關(guān)系，隨機(jī)事件的頻率與概率的區(qū)別與聯(lián)系，并會(huì)計(jì)算；(2)理解互斥事件與對(duì)立事件的區(qū)別與聯(lián)系，并會(huì)利用公式進(jìn)行計(jì)算訓(xùn)練題型(1)利用頻率估計(jì)概率；(2)求互斥事件，對(duì)立事件的概率解題策略(1)根據(jù)頻率與概率的關(guān)系，由頻率直接估計(jì)概率；(2)根據(jù)互斥、對(duì)立事件的定義分析所給的兩個(gè)事件的關(guān)系，再選擇相應(yīng)的公式求解.1容量為20的樣本數(shù)據(jù)，分組后的頻數(shù)如下表：分組10,20)20,30)30,40)40,50)50,60)60,70)頻數(shù)234542則根據(jù)樣本數(shù)據(jù)估計(jì)落在區(qū)間10,40)的概率為_2(2016山西四校聯(lián)考)從1,2,3,4這四個(gè)數(shù)中一次隨機(jī)取兩個(gè)，則取出的兩個(gè)

2、數(shù)之和為偶數(shù)的概率是_3甲：A1、A2是互斥事件；乙：A1、A2是對(duì)立事件那么甲是乙的_條件(填“充分不必要”“必要不充分”“充要”或“既不充分也不必要”)4從1,2，9中任取兩數(shù)，其中：恰有一個(gè)偶數(shù)和恰有一個(gè)奇數(shù)；至少有一個(gè)奇數(shù)和兩個(gè)數(shù)都是奇數(shù)；至少有一個(gè)奇數(shù)和兩個(gè)數(shù)都是偶數(shù)；至少有一個(gè)奇數(shù)和至少有一個(gè)偶數(shù)在上述各對(duì)事件中，是對(duì)立事件的是_5(2016無錫模擬)一只袋子中裝有7個(gè)紅玻璃球，3個(gè)綠玻璃球，從中無放回地任意抽取兩次，每次只取一個(gè)，取得兩個(gè)紅球的概率為，取得兩個(gè)綠球的概率為，則取得兩個(gè)同顏色的球的概率為_；至少取得一個(gè)紅球的概率為_6(2016泰州一模)甲乙兩人下棋，若甲獲勝的概率

3、為，甲乙下成和棋的概率為，則乙不輸棋的概率為_7(2016蘇、錫、常、鎮(zhèn)一模)在一次滿分為160分的數(shù)學(xué)考試中，某班40名學(xué)生的考試成績(jī)分布如下：成績(jī)(分)80分以下80，100)100，120)120，140)140，160人數(shù)8812102從該班學(xué)生中隨機(jī)抽取一名學(xué)生，則該學(xué)生在這次考試中成績(jī)不少于120分的概率為_8(2017沈陽四校聯(lián)考)任取一個(gè)三位正整數(shù)N，則對(duì)數(shù)log2N是一個(gè)正整數(shù)的概率是_9(2016連云港模擬)在數(shù)字1,2,3,4四個(gè)數(shù)中，任取兩個(gè)不同的數(shù)，其和大于積的概率是_10在正六邊形的6個(gè)頂點(diǎn)中隨機(jī)選擇4個(gè)頂點(diǎn)，則構(gòu)成的四邊形是梯形的概率為_11在一場(chǎng)比賽中，某籃球隊(duì)

4、的11名隊(duì)員共有9名隊(duì)員上場(chǎng)比賽，其得分的莖葉圖如圖所示從上述得分超過10分的隊(duì)員中任取2名，則這2名隊(duì)員的得分之和超過35分的概率為_12(2016南通三模)從集合1,2,3,4,5,6,7,8,9中任取一個(gè)數(shù)記為x，則log2x為整數(shù)的概率為_13將一枚骰子(一種六個(gè)面上分別標(biāo)有1,2,3,4,5,6的正方體玩具)先后拋擲2次，向上的點(diǎn)數(shù)分別記為m，n，則點(diǎn)P(m，n)落在區(qū)域|x2|y2|2內(nèi)的概率是_14(2016鎮(zhèn)江模擬)設(shè)m，n分別為連續(xù)兩次投擲骰子得到的點(diǎn)數(shù)，且向量a(m，n)，b(1，1)，則向量a，b的夾角為銳角的概率是_答案精析10.452.3.必要不充分4.5.解析(1)

5、由于“取得兩個(gè)紅球”與“取得兩個(gè)綠球”是互斥事件，取得兩個(gè)同色球，只需兩互斥事件有一個(gè)發(fā)生即可，因而取得兩個(gè)同色球的概率為P.(2)由于事件A“至少取得一個(gè)紅球”與事件B“取得兩個(gè)綠球”是對(duì)立事件，則至少取得一個(gè)紅球的概率為P(A)1P(B)1.6.解析“乙不輸棋”的對(duì)立事件為“甲獲勝”，P(乙不輸棋)1P(甲獲勝).70.3解析成績(jī)不少于120分的學(xué)生有12人，所以抽取的這名學(xué)生在這次考試中的成績(jī)不少于120分的概率為0.38.解析三位正整數(shù)共有900個(gè)，使log2N為正整數(shù)，N為29,28,27共三個(gè)，概率為.9.解析從1,2,3,4中任取兩數(shù)可能為(1,2)，(1,3)，(1,4)，(2

6、,3)，(2,4)，(3,4)，共6個(gè)可能的基本事件，其中和大于積的有(1,2)，(1,3)，(1,4)，故概率為.10.解析如圖為正六邊形ABCDEF，從6個(gè)頂點(diǎn)中隨機(jī)選擇4個(gè)頂點(diǎn)，共有15種選法，其中構(gòu)成的四邊形是梯形的有ABEF、BCDE、ABCF、CDEF、ABCD、ADEF，共6種選法，故構(gòu)成的四邊形是梯形的概率為P.11.解析從得分超過10分的隊(duì)員中任取2名，一共有以下10種不同的取法：(12,14)，(12,15)，(12,20)，(12,22)，(14,15)，(14,20)，(14,22)，(15,20)，(15,22)，(20,22)，其中這2名隊(duì)員的得分之和超過35分的取法有以下3種：(14,22)，(15,22)，(20,22)，故所求概率P.12.解析能使log2x為整數(shù)的x有1,2,4,8，所以P.13.解析由題意可得所有可能的基本事件共36個(gè)當(dāng)m1時(shí)，1n3，故符合條件的基本事件有3個(gè)；當(dāng)m2時(shí)，1n4，故符合條件的基本事件有4個(gè)；當(dāng)m3時(shí)，1n3，故符合條件的基本事件有3個(gè)；當(dāng)m4時(shí)，n2，故符合條件的基本事件有1個(gè)故共有11個(gè)符合條件的基本事件，即所求概率為.14.解析向量a，b的夾角為銳角，所以ab0，所以mn0，即mn.所以P.