浙江省溫州23中2020高二數(shù)學(xué)會考后進生輔導(dǎo)資料 第三講 三角函數(shù)與三角恒等變換

《浙江省溫州23中2020高二數(shù)學(xué)會考后進生輔導(dǎo)資料 第三講 三角函數(shù)與三角恒等變換》由會員分享，可在線閱讀，更多相關(guān)《浙江省溫州23中2020高二數(shù)學(xué)會考后進生輔導(dǎo)資料 第三講 三角函數(shù)與三角恒等變換（4頁珍藏版）》請在裝配圖網(wǎng)上搜索。

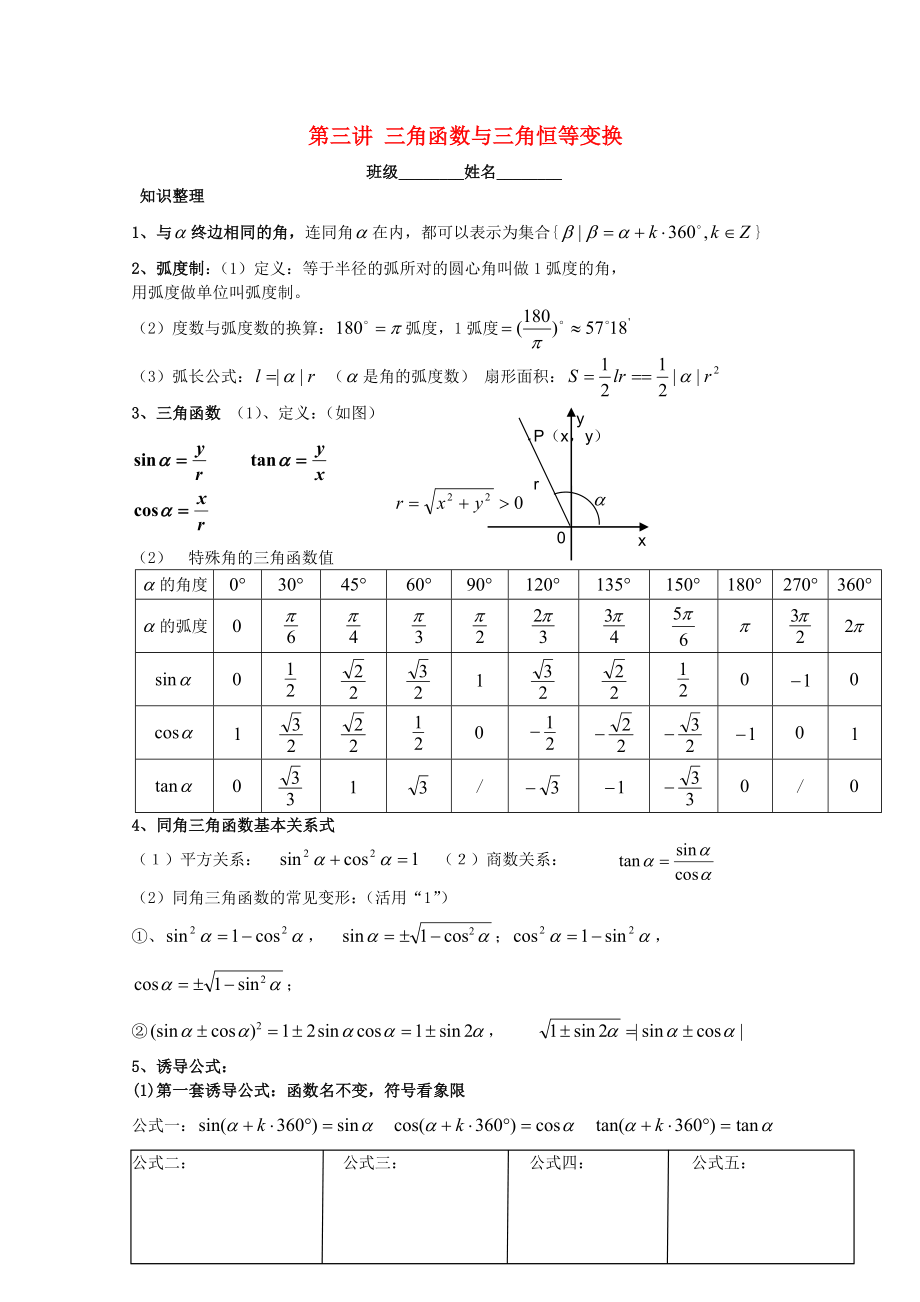
1、第三講 三角函數(shù)與三角恒等變換班級_姓名_知識整理1、與終邊相同的角，連同角在內(nèi)，都可以表示為集合2、弧度制：（1）定義：等于半徑的弧所對的圓心角叫做1弧度的角，用弧度做單位叫弧度制。（2）度數(shù)與弧度數(shù)的換算：弧度，1弧度（3）弧長公式： （是角的弧度數(shù)） 扇形面積：P（x，y）rx0y3、三角函數(shù) （1）、定義：（如圖） （2）特殊角的三角函數(shù)值的角度的弧度/4、同角三角函數(shù)基本關(guān)系式（）平方關(guān)系：（）商數(shù)關(guān)系： （2）同角三角函數(shù)的常見變形：（活用“1”）、，；，；， 5、誘導(dǎo)公式：(1)第一套誘導(dǎo)公式：函數(shù)名不變，符號看象限公式一：公式二： 公式三： 公式四： 公式五： (2) 第二套誘

2、導(dǎo)公式：函數(shù)名改變，符號看象限6、兩角和與差的正弦、余弦、正切 的整式形式為：7、輔助角公式：（其中稱為輔助角，的終邊過點，） （多用于研究性質(zhì)）8、二倍角公式（1） （2）降冪公式： 9、三角函數(shù)的圖象性質(zhì)函數(shù)定義域值域周期性奇偶性遞增區(qū)間遞減區(qū)間-1，1奇函數(shù)-1，1偶函數(shù)（-,+）奇函數(shù)圖象的五個關(guān)鍵點：（0，0），（，1），（，0），（，-1），（，0）；圖象的五個關(guān)鍵點：（0，1），（，0），（，-1），（，0），（，1）；的對稱中心為（）；對稱軸是直線； 的周期；的對稱中心為（）；對稱軸是直線； 的周期；的對稱中心為點（）和點（）； 的周期；練習(xí)訓(xùn)練1、下列角中，終邊在第四象限的角

3、是 ( )(A)- (B) (C)- (D)2、 （ ） A. B. C. D. 3、已知sin=，且是第一象限的角，則cos(-)= ( ) (A) (B) (C) (D)4、角的終邊經(jīng)過點P(3，4)，則sin= ( ) (A) (B) (C) (D)5、已知cos=1，02，則= ( ) (A)0 (B) (C)(D) 6、下列說法正確的是 （ ）(A)終邊相同的角一定相等 (B)銳角是第一象限角(C)第二象限角為鈍角 (D)小于的角一定為銳角 7、已知，則cosa= ( )(A)- (B) (C) (D)8、函數(shù) y = cos x， -，的值域是 ( )（A）0，1 （B）-1，1

4、（C）0，（D）-，19、函數(shù)取得最大值時的一個x值是 ( )(A) (B) (C) (D)010、f ( x ) = sin 是 ( )（A）最小正周期為的奇函數(shù) （B）最小正周期為4的奇函數(shù)（C）最小正周期為的偶函數(shù) （D）最小正周期為4的偶函數(shù)11、將函數(shù)ycos(x)的圖象經(jīng)過怎樣的平移，可以得到函數(shù)ycos(x)的圖（ ）(A) 向左平移個單位長度 (B) 向右平移個單位長度(C) 向右平移個單位長度 (D) 向左平移個單位長度12、函數(shù)y=cos2 xsin2x的最小正周期是 ( ) A. 4 B. 2 C. D. 13、已知，為第三象限角，則=_14、_15、右圖表示周期函數(shù)y=f(x)的變化規(guī)律，由圖象可以觀察 出f(x)的最小正周期是_（第19題）16、如圖，單擺的擺球離開平衡位置的位移S（厘米）和 時間 t （秒）的函數(shù)關(guān)系是，則擺球往復(fù)擺動一次所需要的時間是 秒17、已知tana=，求=_18、已知sin=，90o180o，(1) tan (2) (3) cos2