（新課標(biāo)）2021版高考數(shù)學(xué)一輪總復(fù)習(xí) 第二章 函數(shù) 第4講 函數(shù)及其表示導(dǎo)學(xué)案 新人教A版

《（新課標(biāo)）2021版高考數(shù)學(xué)一輪總復(fù)習(xí) 第二章 函數(shù) 第4講 函數(shù)及其表示導(dǎo)學(xué)案 新人教A版》由會員分享，可在線閱讀，更多相關(guān)《（新課標(biāo)）2021版高考數(shù)學(xué)一輪總復(fù)習(xí) 第二章 函數(shù) 第4講 函數(shù)及其表示導(dǎo)學(xué)案 新人教A版（11頁珍藏版）》請在裝配圖網(wǎng)上搜索。

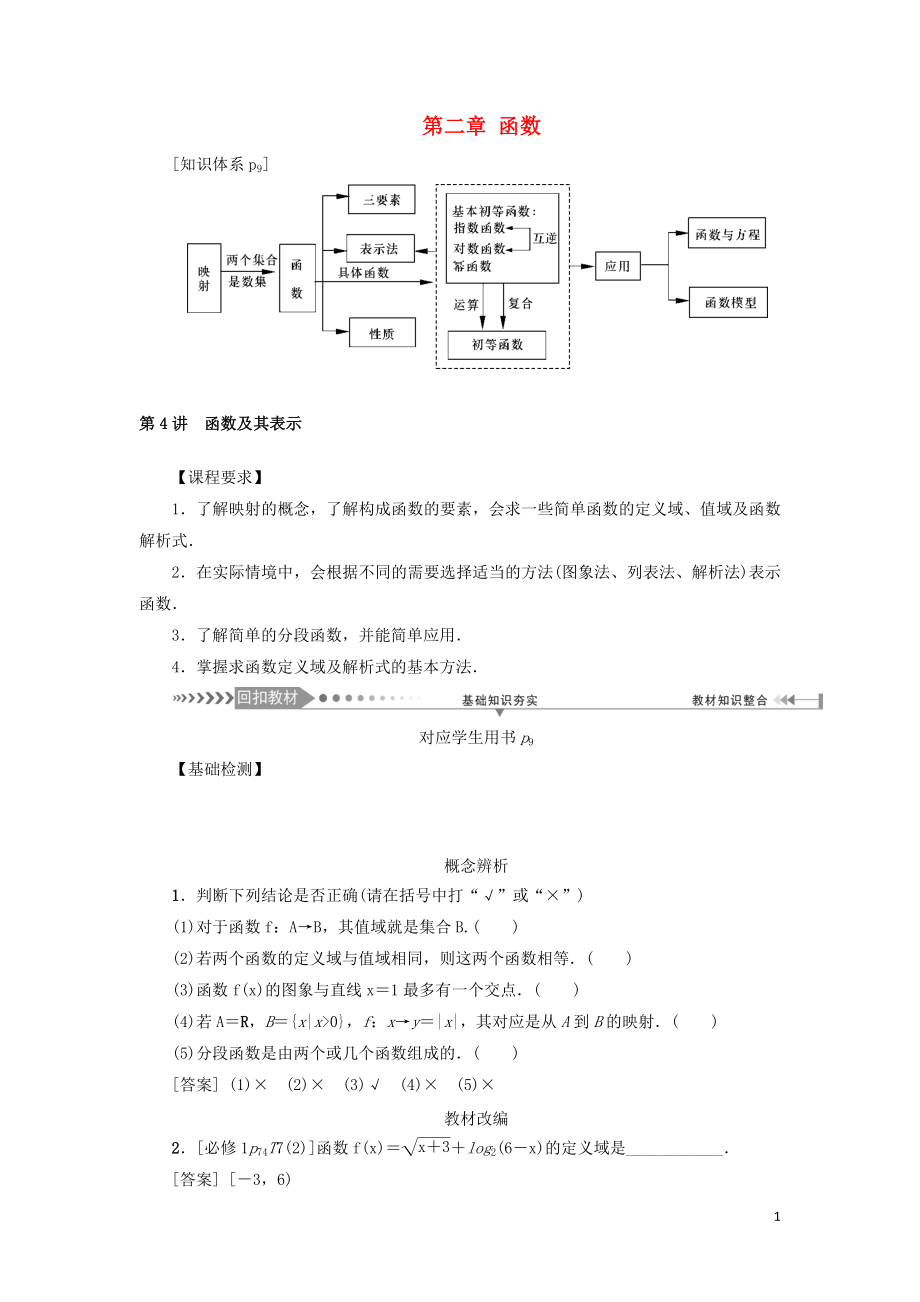
1、第二章 函數(shù)知識體系p9第4講函數(shù)及其表示【課程要求】1了解映射的概念，了解構(gòu)成函數(shù)的要素，會求一些簡單函數(shù)的定義域、值域及函數(shù)解析式2在實際情境中，會根據(jù)不同的需要選擇適當(dāng)?shù)姆椒?圖象法、列表法、解析法)表示函數(shù)3了解簡單的分段函數(shù)，并能簡單應(yīng)用4掌握求函數(shù)定義域及解析式的基本方法對應(yīng)學(xué)生用書p9【基礎(chǔ)檢測】1判斷下列結(jié)論是否正確(請在括號中打“”或“”)(1)對于函數(shù)f：AB，其值域就是集合B.()(2)若兩個函數(shù)的定義域與值域相同，則這兩個函數(shù)相等()(3)函數(shù)f(x)的圖象與直線x1最多有一個交點()(4)若AR，Bx|x0，f：xy|x|，其對應(yīng)是從A到B的映射()(5)分段函數(shù)是由

2、兩個或幾個函數(shù)組成的()答案 (1)(2)(3)(4)(5)2必修1p74T7(2)函數(shù)f(x)log2(6x)的定義域是_答案 3，6)3必修1p25B組T1函數(shù)yf(x)的圖象如圖所示，那么，f(x)的定義域是_；值域是_；其中只有唯一的x值與之對應(yīng)的y值的范圍是_答案 3，02，3；1，5；1，2)(4，54已知函數(shù)f(x)的定義域為0，2，則函數(shù)f(2x)的定義域為()Ax|0x4Bx|0x4Cx|0x1Dx|0x1解析因為函數(shù)f(x)的定義域為0，2，所以02x2，解得0x1，所以函數(shù)f(2x)的定義域為x|0x1答案D5已知fx2x，則f_解析設(shè)t2x1，則x，f，即f.答案6已知

3、f(x)若f(a)2，則a的值為_解析當(dāng)a0時，2a22，解得a2；當(dāng)a0在R上恒成立，當(dāng)m0時，有10在R上恒成立，故符合條件；當(dāng)m0時，由解得0m0，解得0x2，故其定義域是0，2)答案B4已知函數(shù)yf(x21)的定義域為，則函數(shù)yf(x)的定義域為_解析因為函數(shù)yf(x21)的定義域為，所以x，所以1x212，所以函數(shù)yf(x)的定義域為1，2答案 1，2函數(shù)的解析式例3(1)已知f4x26x5，則f_解析法一：f3，fx2x3，即函數(shù)的解析式為fx2x3.法二：令t2x1，則x.f465t2t3，fx2x3，即為所求的解析式答案x2x3(2)如圖，修建一條公路需要一段環(huán)湖彎曲路段與兩條

4、直道平滑連接(相切)已知環(huán)湖彎曲路段為某三次函數(shù)圖象的一部分，則該函數(shù)的解析式為()Ayx3x2xByx3x23xCyx3xDyx3x22x解析設(shè)所求函數(shù)解析式為f(x)ax3bx2cxd(a0)，則f(x)3ax22bxc(a0)，由題意知解得f(x)x3x2x.答案A小結(jié)求函數(shù)解析式的幾種常用方法：(1)待定系數(shù)法：若已知函數(shù)的類型(如一次函數(shù)、二次函數(shù))，根據(jù)函數(shù)類型設(shè)出函數(shù)解析式，根據(jù)題設(shè)條件，列出方程組，解出待定系數(shù)即可(2)配湊法：由已知條件f(g(x)F(x)，可將F(x)改寫成關(guān)于g(x)的表達(dá)式，然后以x替代g(x)，便可得f(x)的解析式；(3)換元法：已知f(h(x)g(

5、x)求f(x)時，往往可設(shè)h(x)t，從中解出x，代入g(x)進(jìn)行換元，求出f(t)的解析式，再將t替換為x即可(4)解方程組法：已知關(guān)于f(x)與f(或f(x)的表達(dá)式，可根據(jù)已知條件再構(gòu)造出另一個方程構(gòu)成方程組求出f(x)配湊法和換元法中要注意根據(jù)g(x)或t的范圍確定函數(shù)的定義域5已知函數(shù)f(x)x22x1，函數(shù)yg(x)為一次函數(shù)，若g(f(x)2x24x3，則g(x)_解析由題意，函數(shù)yg(x)為一次函數(shù)，由待定系數(shù)法，設(shè)g(x)kxb (k0)，g(f(x)k(x22x1)bkx22kxbk2x24x3，由對應(yīng)系數(shù)相等，得所以k2，b5.故g(x)2x5.答案2x56已知函數(shù)f(x

6、)的定義域為(0，)，且f(x)2f1，則f(x)_解析在f(x)2f1中，將x換成，則換成x，得f2f(x)1，由解得f(x).答案(x0)分段函數(shù)例4(1)已知函數(shù)f(x)若f(a)f(1)0，則實數(shù)a的值等于()A3B1C1D3解析根據(jù)題意，由于函數(shù)f(x)若f(a)f(1)0，而f(1)2，f(a)2，則可知a12，a3.答案D(2)已知函數(shù)f(x)當(dāng)t0，1時，f(f(t)0，1，則實數(shù)t的取值范圍是_解析當(dāng)t0時，f(t)1，f(f(t)f(1)30，1，所以t(0，1，所以f(t)3t(1，3，所以f(f(t)f(3t)3t0，1，即3t3.所以log3t1.故實數(shù)t的取值范圍是

7、.答案小結(jié)(1)分段函數(shù)問題一般分段求解，其定義域和值域是各段的并集；(2)求分段函數(shù)的函數(shù)值，首先要確定自變量的范圍，然后選定相應(yīng)關(guān)系式代入求解；(3)當(dāng)給出函數(shù)值或函數(shù)值的取值范圍求自變量的值或自變量的取值范圍時，應(yīng)根據(jù)每一段解析式分別求解，但要注意檢驗所求自變量的值或取值范圍是否符合相應(yīng)段的自變量的值或取值范圍；(4)當(dāng)自變量含參數(shù)或范圍不確定時，要根據(jù)定義域分成的不同子集進(jìn)行分類討論7已知函數(shù)f(x)且f(a)3，則f(6a)等于()ABCD解析函數(shù)f(x)且f(a)3，若a1，則2a123，即有2a111，則log2(a1)3，解得a7，則f(6a)f(1)2112.答案A8設(shè)函數(shù)f(x)g(x)為定義在R上的奇函數(shù)，且當(dāng)x0，則x0，由題意，知f(2)2，f(g(a)2即為f(g(a)f(2)又f(x)g(a)2，或或a0，a1或0a21.故選A.答案A對應(yīng)學(xué)生用書p11(2017全國卷理)設(shè)函數(shù)f(x)則滿足f(x)f1的x的取值范圍是_解析當(dāng)x時，f(x)f2x2x2x1；當(dāng)0x時，f(x)f2x12xx2x1；當(dāng)x0時，f(x)fx112x，由f(x)f1，得2x1，即x，即x0.綜上，x.答案11