2018版高中數(shù)學(xué) 第二章 圓錐曲線與方程章末復(fù)習(xí)課學(xué)案 新人教B版選修2-1

《2018版高中數(shù)學(xué) 第二章 圓錐曲線與方程章末復(fù)習(xí)課學(xué)案 新人教B版選修2-1》由會(huì)員分享，可在線閱讀，更多相關(guān)《2018版高中數(shù)學(xué) 第二章 圓錐曲線與方程章末復(fù)習(xí)課學(xué)案 新人教B版選修2-1（7頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

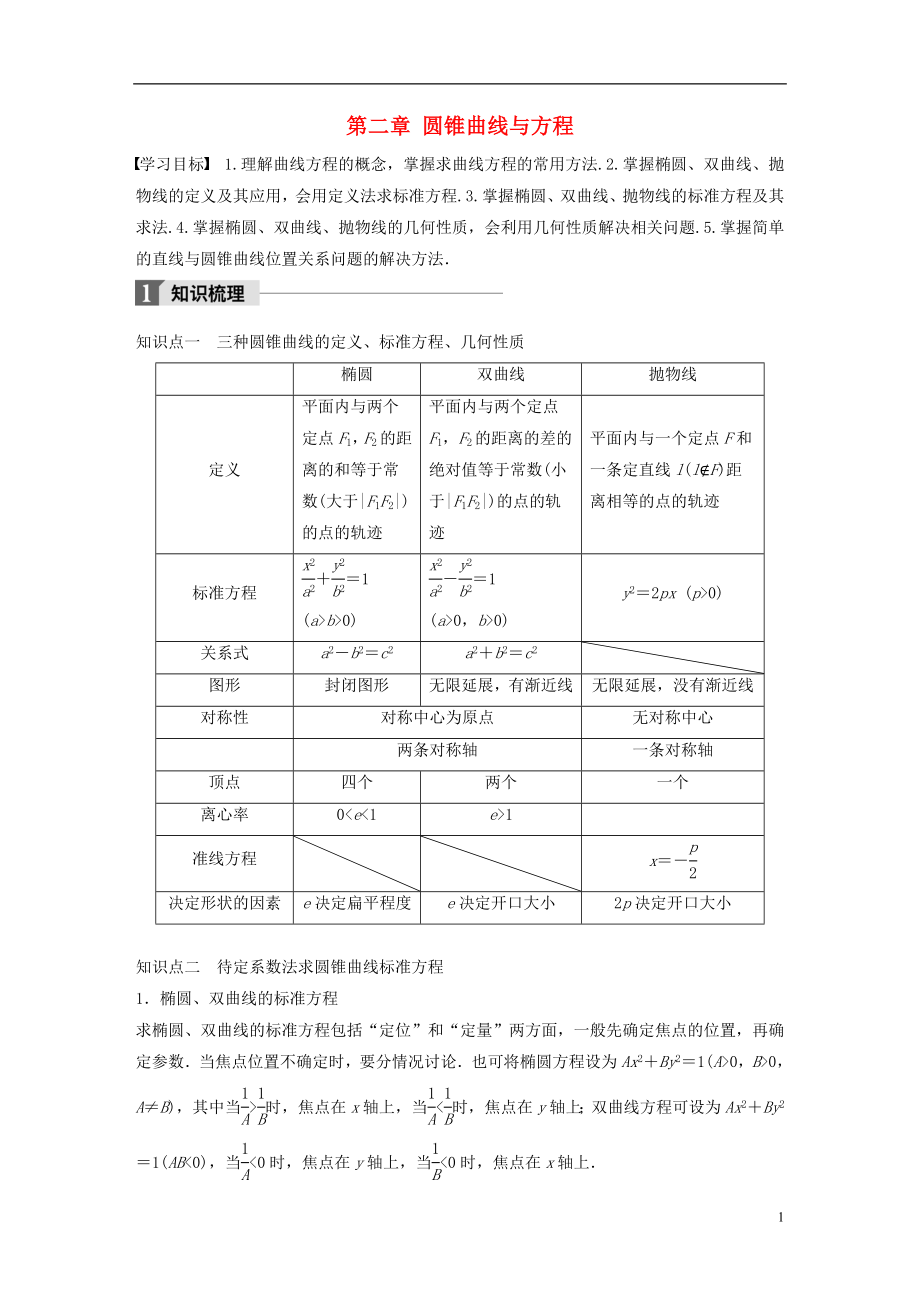
1、第二章 圓錐曲線與方程學(xué)習(xí)目標(biāo)1.理解曲線方程的概念，掌握求曲線方程的常用方法.2.掌握橢圓、雙曲線、拋物線的定義及其應(yīng)用，會(huì)用定義法求標(biāo)準(zhǔn)方程.3.掌握橢圓、雙曲線、拋物線的標(biāo)準(zhǔn)方程及其求法.4.掌握橢圓、雙曲線、拋物線的幾何性質(zhì)，會(huì)利用幾何性質(zhì)解決相關(guān)問(wèn)題.5.掌握簡(jiǎn)單的直線與圓錐曲線位置關(guān)系問(wèn)題的解決方法知識(shí)點(diǎn)一三種圓錐曲線的定義、標(biāo)準(zhǔn)方程、幾何性質(zhì)橢圓雙曲線拋物線定義平面內(nèi)與兩個(gè)定點(diǎn)F1，F(xiàn)2的距離的和等于常數(shù)(大于|F1F2|)的點(diǎn)的軌跡平面內(nèi)與兩個(gè)定點(diǎn)F1，F(xiàn)2的距離的差的絕對(duì)值等于常數(shù)(小于|F1F2|)的點(diǎn)的軌跡平面內(nèi)與一個(gè)定點(diǎn)F和一條定直線l(lF)距離相等的點(diǎn)的軌跡標(biāo)準(zhǔn)方程

2、1(ab0)1 (a0，b0)y22px (p0)關(guān)系式a2b2c2a2b2c2圖形封閉圖形無(wú)限延展，有漸近線無(wú)限延展，沒(méi)有漸近線對(duì)稱性對(duì)稱中心為原點(diǎn)無(wú)對(duì)稱中心兩條對(duì)稱軸一條對(duì)稱軸頂點(diǎn)四個(gè)兩個(gè)一個(gè)離心率0e1準(zhǔn)線方程x決定形狀的因素e決定扁平程度e決定開(kāi)口大小2p決定開(kāi)口大小知識(shí)點(diǎn)二待定系數(shù)法求圓錐曲線標(biāo)準(zhǔn)方程1橢圓、雙曲線的標(biāo)準(zhǔn)方程求橢圓、雙曲線的標(biāo)準(zhǔn)方程包括“定位”和“定量”兩方面，一般先確定焦點(diǎn)的位置，再確定參數(shù)當(dāng)焦點(diǎn)位置不確定時(shí)，要分情況討論也可將橢圓方程設(shè)為Ax2By21(A0，B0，AB)，其中當(dāng)時(shí)，焦點(diǎn)在x軸上，當(dāng)時(shí)，焦點(diǎn)在y軸上；雙曲線方程可設(shè)為Ax2By21(AB0)，當(dāng)0時(shí)

3、，焦點(diǎn)在y軸上，當(dāng)0，b0)共漸近線的雙曲線方程可設(shè)為(0)；已知所求雙曲線為等軸雙曲線，其方程可設(shè)為x2y2(0)2拋物線的標(biāo)準(zhǔn)方程求拋物線的標(biāo)準(zhǔn)方程時(shí)，先確定拋物線的方程類型，再由條件求出參數(shù)p的大小當(dāng)焦點(diǎn)位置不確定時(shí)，要分情況討論，也可將方程設(shè)為y22px(p0)或x22py(p0)，然后建立方程求出參數(shù)p的值知識(shí)點(diǎn)三直線與圓錐曲線有關(guān)的問(wèn)題1直線與圓錐曲線的位置關(guān)系，可以通過(guò)討論直線方程與曲線方程組成的方程組的實(shí)數(shù)解的個(gè)數(shù)來(lái)確定，通常消去方程組中變量y(或x)得到關(guān)于變量x(或y)的一元二次方程，考慮該一元二次方程的判別式，則有：0直線與圓錐曲線相交于兩點(diǎn)；0直線與圓錐曲線相切于一點(diǎn)；

4、0)的焦點(diǎn)為F，點(diǎn)P在C上且其橫坐標(biāo)為1，以F為圓心、|FP|為半徑的圓與C的準(zhǔn)線l相切(1)求p的值；(2)設(shè)l與x軸交點(diǎn)為E，過(guò)點(diǎn)E作一條直線與拋物線C交于A，B兩點(diǎn)，求線段AB的垂直平分線在x軸上的截距的取值范圍1下列各對(duì)方程中，表示相同曲線的一對(duì)方程是()Ay與y2xB.1與lg(y1)lg(x2)Cx2y21與|y|Dylg x2與y2lg x2中心在原點(diǎn)，焦點(diǎn)在x軸上，若長(zhǎng)軸長(zhǎng)為18，且兩個(gè)焦點(diǎn)恰好將長(zhǎng)軸三等分，則此橢圓的方程是()A.1 B.1C.1 D.13設(shè)橢圓1(m0，n0)的右焦點(diǎn)與拋物線y28x的焦點(diǎn)相同，離心率為，則此橢圓的方程為()A.1 B.1C.1 D.14點(diǎn)P

5、(8，1)平分雙曲線x24y24的一條弦，則這條弦所在直線的方程是_5直線yx3與曲線1交點(diǎn)的個(gè)數(shù)為_(kāi)1離心率的幾種求法(1)定義法：由橢圓(雙曲線)的標(biāo)準(zhǔn)方程可知，不論橢圓(雙曲線)的焦點(diǎn)在x軸上還是在y軸上都有關(guān)系式a2b2c2(a2b2c2)以及e，已知其中的任意兩個(gè)參數(shù)，可以求其他的參數(shù)，這是基本且常用的方法(2)方程法：建立參數(shù)a與c之間的齊次關(guān)系式，從而求出離心率，這是求離心率十分重要的方法(3)幾何法：與過(guò)焦點(diǎn)的三角形有關(guān)的離心率問(wèn)題，根據(jù)平面幾何性質(zhì)、橢圓(雙曲線)的幾何性質(zhì)和定義，建立參數(shù)之間的關(guān)系2圓錐曲線中的有關(guān)最值問(wèn)題在解決與圓錐曲線有關(guān)的最值問(wèn)題時(shí)，通常的處理策略(1

6、)若具備定義的最值問(wèn)題，可用定義將其轉(zhuǎn)化為幾何問(wèn)題來(lái)處理(2)一般問(wèn)題可由條件建立目標(biāo)函數(shù)，然后利用函數(shù)求最值的方法進(jìn)行求解如利用二次函數(shù)在閉區(qū)間上最值的求法，利用函數(shù)的單調(diào)性，亦可利用均值不等式等求解提醒：完成作業(yè)第二章章末復(fù)習(xí)課答案精析題型探究例18解析如圖，設(shè)點(diǎn)B為橢圓的左焦點(diǎn)，點(diǎn)M(2，1)在橢圓內(nèi)，那么|BM|AM|AC|AB|AC|2a，所以|AM|AC|2a|BM|，而a4，|BM|，所以(|AM|AC|)最小值8.跟蹤訓(xùn)練1D例2跟蹤訓(xùn)練2C例3解假設(shè)在x軸上存在點(diǎn)M(m，0)，使為常數(shù)設(shè)A(x1，y1)，B(x2，y2)當(dāng)直線AB與x軸不垂直時(shí)，直線AB的斜率存在，設(shè)直線AB

7、的方程為yk(x1)，將yk(x1)代入橢圓方程x23y25，消去y整理，得(3k21)x26k2x3k250.則所以(x1m)(x2m)y1y2(x1m)(x2m)k2(x11)(x21)(k21)x1x2(k2m)(x1x2)k2m2.將上式整理，得m2m2m22m.注意到是與k無(wú)關(guān)的常數(shù)，從而有6m140，解得m，此時(shí).當(dāng)直線AB與x軸垂直時(shí)，此時(shí)點(diǎn)A，B的坐標(biāo)分別為A(1，)，B(1，)，當(dāng)m時(shí)，亦有.綜上，在x軸上存在定點(diǎn)M(，0)，使為常數(shù)跟蹤訓(xùn)練3解(1)因?yàn)橐訤為圓心、|FP|為半徑的圓與C的準(zhǔn)線l相切，所以圓的半徑為p，即|FP|p，所以FPx軸，又點(diǎn)P的橫坐標(biāo)為1，所以焦點(diǎn)F的坐標(biāo)為(1，0)，從而p2.(2)由(1)知拋物線C的方程為y24x，設(shè)A(x1，y1)，B(x2，y2)，線段AB的垂直平分線與x軸的交點(diǎn)D(x0，0)，則由|DA|DB|，y4x1，y4x2，得(x1x0)2y(x2x0)2y，化簡(jiǎn)得x02，設(shè)直線AB的方程為xmy1，代入拋物線C的方程，得y24my40，由0得m21，由根與系數(shù)的關(guān)系得y1y24m，所以x1x2m(y1y2)24m22，代入得x02m213，故線段AB的垂直平分線在x軸上的截距的取值范圍是(3，)當(dāng)堂訓(xùn)練1C2.A3.B42xy1505.37