《2018年秋八年級數(shù)學上冊 第14章 全等三角形 14.2 三角形全等的判定 第3課時 三邊分別相等的兩個三角形作業(yè) （新版）滬科版》由會員分享，可在線閱讀，更多相關(guān)《2018年秋八年級數(shù)學上冊 第14章 全等三角形 14.2 三角形全等的判定 第3課時 三邊分別相等的兩個三角形作業(yè) （新版）滬科版（5頁珍藏版）》請在裝配圖網(wǎng)上搜索。
1、
第3課時 三邊分別相等的兩個三角形
知識要點基礎(chǔ)練
知識點1 判定三角形全等的方法——“SSS”
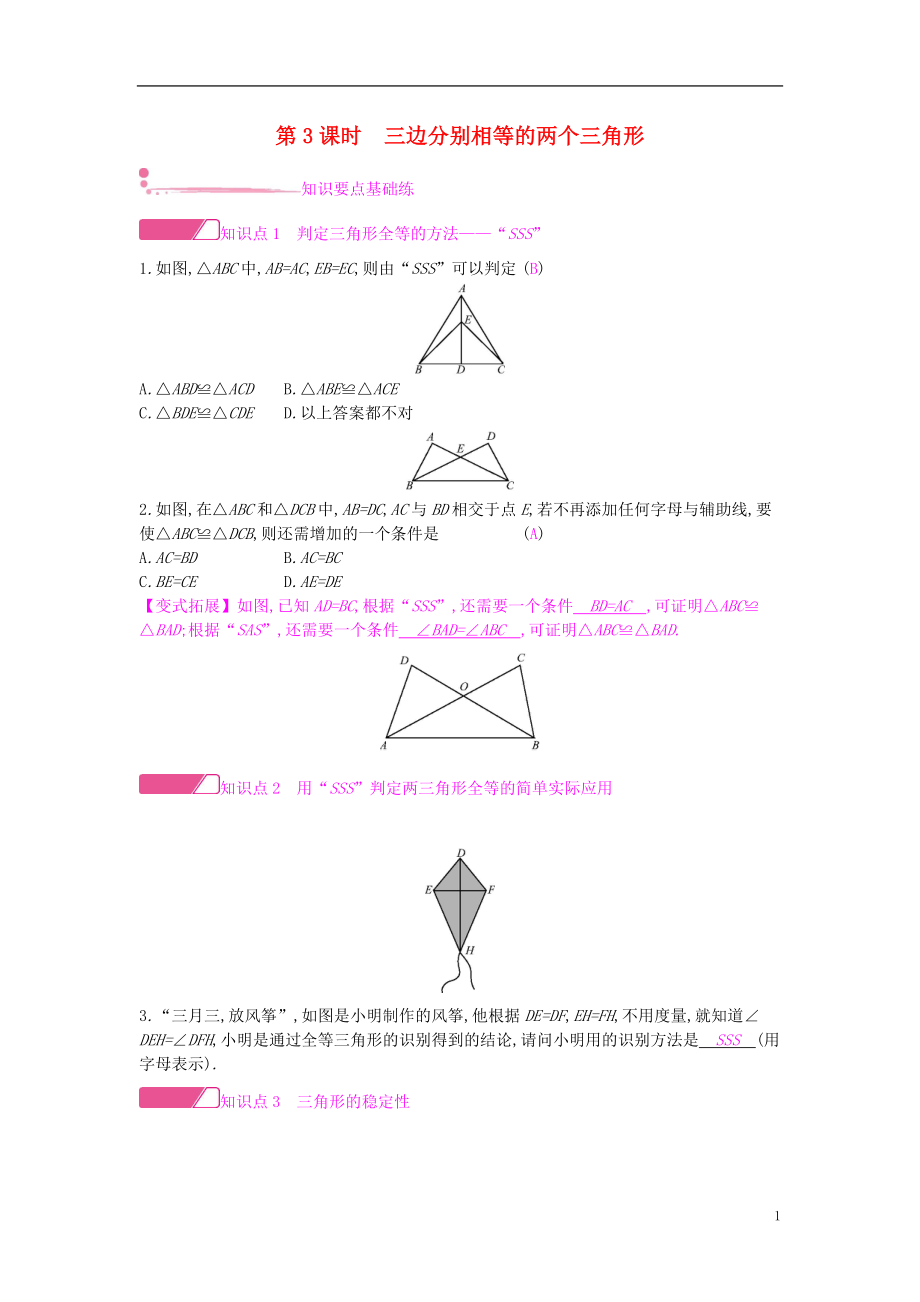
1.如圖,△ABC中,AB=AC,EB=EC,則由“SSS”可以判定 (B)
A.△ABD≌△ACD B.△ABE≌△ACE
C.△BDE≌△CDE D.以上答案都不對
2.如圖,在△ABC和△DCB中,AB=DC,AC與BD相交于點E,若不再添加任何字母與輔助線,要使△ABC≌△DCB,則還需增加的一個條件是 (A)
A.AC=BD B.AC=BC
C.BE=CE D.AE=DE
【變式拓展】如圖,已知AD=BC,根據(jù)“SSS”,還需要一個條件 BD=AC ,可證明
2、△ABC≌△BAD;根據(jù)“SAS”,還需要一個條件 ∠BAD=∠ABC ,可證明△ABC≌△BAD.?
知識點2 用“SSS”判定兩三角形全等的簡單實際應用
3.“三月三,放風箏”,如圖是小明制作的風箏,他根據(jù)DE=DF,EH=FH,不用度量,就知道∠DEH=∠DFH,小明是通過全等三角形的識別得到的結(jié)論,請問小明用的識別方法是 SSS (用字母表示).?
知識點3 三角形的穩(wěn)定性
4.為了使一扇舊木門不變形,木工師傅在木門的背面加釘了一根木條,這樣做的道理是 (C)
A.兩點之間,線段最短
B.垂線段最短
C.三角形具有穩(wěn)定性
D.兩直線平行,內(nèi)錯角相等
3、
知識點4 用“SSS”判定兩三角形全等的推理證明的應用
5.如圖,AF=DB,BC=EF,AC=ED,求證:CB∥EF.
證明:∵AF=DB,
∴AF+FB=DB+FB,即AB=DF.
在△ACB和△DEF中,
∴△ACB≌△DEF(SSS).
∴∠ABC=∠DFE.
∴CB∥EF.
綜合能力提升練
6.如圖,工人師傅做了一個長方形窗框ABCD,E,F,G,H分別是四條邊上的中點,為了使它穩(wěn)固,需要在窗框上釘一根木條,這根木條不應釘在 (B)
A.A,C兩點之間 B.E,G兩點之間
C.B,F兩點之間 D.G,H兩點之間
7.如圖,AB=AD,AC=AE,
4、BC=DE,∠A=60°,∠E=30°,則∠EBC的度數(shù)為 (C)
A.60°
B.75°
C.90°
D.120°
8.在如圖所示的5×5方格中,每個小方格都是邊長為1的正方形,△ABC是格點三角形(即頂點恰好是正方形的頂點),則與△ABC有一條公共邊且全等的所有格點三角形的個數(shù)是 (D)
A.1 B.2 C.3 D.4
9.如圖所示,一扇窗戶打開后,用窗鉤AB可將其固定,這里所運用的幾何原理是 三角形的穩(wěn)定性 .?
10.小聰用刻度尺畫已知角的平分線,如圖,在∠MAN兩邊上分別量取AB=AC,AE=AF,連接FC,EB,交于點D,作射線AD,則圖中共有
5、4 對全等三角形.?
11.如圖,已知線段AB,CD相交于點O,AD,CB的延長線交于點E,OA=OC,EA=EC.
(1)求證:∠A=∠C.
(2)在(1)的證明過程中,需要作輔助線,它的意圖是什么?
解:(1)連接OE.
在△EAO和△ECO中,
∴△EAO≌△ECO(SSS).
∴∠A=∠C(全等三角形的對應角相等).
(2)構(gòu)造全等三角形.
12.如圖,C,F是線段BE上的兩點,△ABF≌△DEC,且AC=DF.
(1)你在圖中還能找到幾對全等的三角形?并說明理由;
(2)∠ACE=∠BFD嗎?試說明你的理由.
解:(1)還能找到2對全等三角
6、形,分別是△ACF≌△DFC,△ABC≌△DEF.理由如下:
∵△ABF≌△DEC,
∴AB=DE,BF=EC,AF=DC.
∴BF+FC=EC+FC,即BC=EF.
在△ACF和△DFC中,
∵AC=DF,AF=DC,FC=CF,
∴△ACF≌△DFC(SSS).
在△ABC和△DEF中,
∵AB=DE,AC=DF,BC=EF,
∴△ABC≌△DEF(SSS).
(2)∠ACE=∠BFD.理由如下:
∵△ABC≌△DEF,
∴∠ACB=∠DFE.
∵∠ACB+∠ACE=180°,
∠DFE+∠BFD=180°,
∴∠ACE=∠BFD.
拓展探究突破練
13.數(shù)學家魯弗斯設(shè)計了一個儀器,它可以三等分一個角.如圖所示,A,B,C,D分別固定在以O(shè)為公共端點的四根木條上,且OA=OB=OC=OD,E,F可以在中間的兩根木條上滑動,AE=CE=BF=DF.
求證:∠AOE=∠EOF=∠FOD.
證明:在△AOE和△COE中,
∴△AOE≌△COE(SSS),
∴∠AOE=∠EOF,
同理∠EOF=∠FOD,
∴∠AOE=∠EOF=∠FOD.
5
2018年秋八年級數(shù)學上冊 第14章 全等三角形 14.2 三角形全等的判定 第3課時 三邊分別相等的兩個三角形作業(yè) （新版）滬科版
