《(江蘇專用)高考數(shù)學(xué)大一輪復(fù)習(xí) 第八章 第48課 基本不等式及其應(yīng)用(二)檢測評估-人教版高三全冊數(shù)學(xué)試題》由會(huì)員分享,可在線閱讀����,更多相關(guān)《(江蘇專用)高考數(shù)學(xué)大一輪復(fù)習(xí) 第八章 第48課 基本不等式及其應(yīng)用(二)檢測評估-人教版高三全冊數(shù)學(xué)試題(6頁珍藏版)》請?jiān)谘b配圖網(wǎng)上搜索。
1�、第48課 基本不等式及其應(yīng)用(二)
一、 填空題
1. 已知函數(shù)y=x-3+(x>-1).若當(dāng)x=a時(shí),該函數(shù)取得最小值b,則a+b= .
2. (2014·四川卷)設(shè)m∈R,過定點(diǎn)A的動(dòng)直線x+my=0和過定點(diǎn)B的動(dòng)直線mx-y-m+3=0交于點(diǎn)P(x,y),則PA·PB的最大值是 .
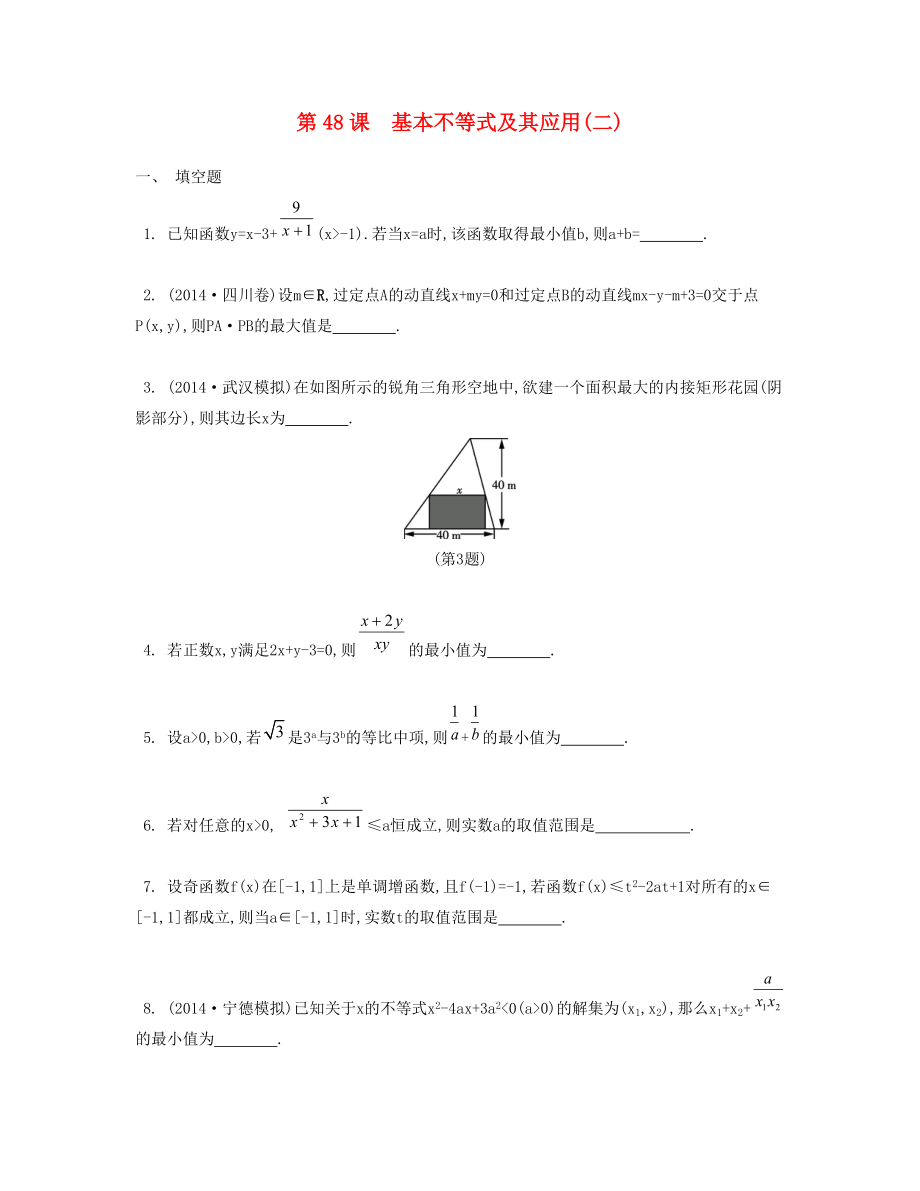
3. (2014·武漢模擬)在如圖所示的銳角三角形空地中,欲建一個(gè)面積最大的內(nèi)接矩形花園(陰影部分),則其邊長x為 .
(第3題)
4. 若正數(shù)x,y滿足2x+y-3=0,則的最小值為 .
5. 設(shè)a>0,b>0,若是3a與3b的等比中項(xiàng)
2����、,則+的最小值為 .
6. 若對任意的x>0, ≤a恒成立,則實(shí)數(shù)a的取值范圍是 .
7. 設(shè)奇函數(shù)f(x)在[-1,1]上是單調(diào)增函數(shù),且f(-1)=-1,若函數(shù)f(x)≤t2-2at+1對所有的x∈[-1,1]都成立,則當(dāng)a∈[-1,1]時(shí),實(shí)數(shù)t的取值范圍是 .
8. (2014·寧德模擬)已知關(guān)于x的不等式x2-4ax+3a2<0(a>0)的解集為(x1,x2),那么x1+x2+的最小值為 .
二��、 解答題
9. (2014·安豐高級(jí)中學(xué))已知在銳角△ABC中,角A,B,C的對邊分別為a,b,c,且(b2+c2-a2)tan
3���、A=bc.
(1) 求角A的大小;
(2) 若a=2,求△ABC面積S的最大值.
10. (2014·湖北模擬)已知拋物線y2=8x的焦點(diǎn)為F,點(diǎn)(x,y)為該拋物線上的動(dòng)點(diǎn),且點(diǎn)A(-2,0),求的取值范圍.
11. 如圖,兩個(gè)工廠A,B相距2 km,點(diǎn)O為AB的中點(diǎn),現(xiàn)要在以O(shè)為圓心���、2 km 為半徑的圓弧MN上的某一點(diǎn)P處建一幢辦公樓,其中MA⊥AB,NB⊥AB.據(jù)測算,此辦公樓受工廠A的“噪音影響度”與距離AP的平方成反比,比例系數(shù)是1;辦公樓受工廠B的“噪音影響度”與距離BP的平方也成反比,比例系數(shù)是4;辦公樓受A,B兩廠的“總噪音影響度”y是受A,B兩廠“噪音影響度
4�、”的和,設(shè)AP為x km.
(1) 求“總噪音影響度”y關(guān)于x的函數(shù)解析式,并求出該函數(shù)的定義域.
(2) 當(dāng)AP為多少時(shí),“總噪音影響度”最小?
(第11題)
第48課 基本不等式及其應(yīng)用(二)
1. 4 解析:y=x-3+=x+1+-4,因?yàn)閤>-1,所以x+1>0,>0,由均值不等式得y=x+1+-4≥2-4=2,當(dāng)且僅當(dāng)x+1=,即x=2時(shí)取等號(hào),所以a=2,b=2,a+b=4.
2. 5 解析:由題意可知,定點(diǎn)A(0,0),B(1,3),且兩條直線互相垂直,則其交點(diǎn)P(x,y)落在以AB為直徑的圓上,所以PA2+PB2=AB2=10,所以PA·PB≤=5
5����、,當(dāng)且僅當(dāng)PA=PB時(shí),等號(hào)成立.
3. 20m 解析:設(shè)矩形花園另一邊長為y m,則=,所以x+y=40,所以面積S=xy≤=400,當(dāng)且僅當(dāng)x=y=20時(shí)等號(hào)成立,即當(dāng)x=20時(shí)面積最大.
4. 3 解析:由2x+y-3=0,得+=1,則=+==+≥×2+=3.
5. 4 解析:由題意知3a×3b=,即3a+b=3,所以a+b=1.所以+=+=2++≥2+2=4,當(dāng)且僅當(dāng)a=b=時(shí)取等號(hào),所以最小值為4.
6. 解析:因?yàn)閤>0,所以x+≥2(當(dāng)且僅當(dāng)x=1時(shí)取等號(hào)),所以=≤=,即的最大值為,故a≥.
7. {t|t≤-2或t=0或t≥2} 解析:因?yàn)?/p>
6、奇函數(shù)f(x)在[-1,1]上是單調(diào)增函數(shù),且f(-1)=-1,所以最大值為f(1)=1,要使f(x)≤t2-2at+1對所有的x∈[-1,1]都成立,則1≤t2-2at+1,即t2-2at≥0,即t(t-2a)≥0,當(dāng)t=0時(shí),不等式成立,當(dāng)0≤a≤1時(shí),不等式的解為t≥2;當(dāng)-1≤a≤0時(shí),不等式的解為t≤-2.
8. 解析:由題意知x1+x2=4a,x1x2=3a2,所以x1+x2+=4a+≥2 =,當(dāng)且僅當(dāng)a=時(shí),等號(hào)成立.
9. (1) 由已知得·=,所以sinA=.
又因?yàn)椤鰽BC為銳角三角形,所以A=60°.
(2) 因?yàn)閍=2,A=60°,所以b2+c2=b
7��、c+4,
S=bcsinA=bc.
又b2+c2≥2bc,所以bc+4≥2bcTbc≤4,
所以S=bc≤×4=,
所以△ABC面積S的最大值為.
10. 由拋物線的定義可得PF=x+2,
又PA==,
所以==,
當(dāng)x=0時(shí),=1;
當(dāng)x≠0時(shí),=,
因?yàn)閤+≥2=4,當(dāng)且僅當(dāng)x=,即x=2時(shí)取等號(hào),所以x++4≥8,所以≤1,
所以∈(1,].
綜上,的取值范圍是[1,].
11. (1) 連接OP,設(shè)∠AOP=α,則≤α≤.
在△AOP中,由余弦定理得x2=12+22-2×1×2×cosα=5-4cosα,
在△BOP中,由余弦定理得BP2=12+2
8���、2-2×1×2×cos(π-α)=5+4cosα,
所以BP2=10-x2,則y=+=+.
因?yàn)椤堞痢?所以-≤cosα≤,
所以3≤5-4cosα≤7,即≤x≤.
所以y=+,定義域?yàn)閇,].
(2) 方法一:由(1)得y=+=(+)·[x2+(10-x2)]=≥=,
當(dāng)且僅當(dāng)=,即x2=時(shí)取等號(hào),此時(shí)x=∈[,].
故當(dāng)AP為km時(shí),“總噪音影響度”最小.
方法二:令t=x2,則y=+(3≤t≤7),
所以y'=+==.
令y'=0,得t=或t=-10(舍去).
當(dāng)t∈時(shí),y'<0,函數(shù)單調(diào)遞減;
當(dāng)t∈時(shí),y'>0,函數(shù)單調(diào)遞增.
所以當(dāng)t=,即x=∈[,]時(shí),y有最小值.
故當(dāng)AP為km時(shí),“總噪音影響度”最小.
 (江蘇專用)高考數(shù)學(xué)大一輪復(fù)習(xí) 第八章 第48課 基本不等式及其應(yīng)用(二)檢測評估-人教版高三全冊數(shù)學(xué)試題
(江蘇專用)高考數(shù)學(xué)大一輪復(fù)習(xí) 第八章 第48課 基本不等式及其應(yīng)用(二)檢測評估-人教版高三全冊數(shù)學(xué)試題