安徽省2022中考數(shù)學(xué)決勝二輪復(fù)習(xí) 專題三 圖表信息問題習(xí)題

《安徽省2022中考數(shù)學(xué)決勝二輪復(fù)習(xí) 專題三 圖表信息問題習(xí)題》由會員分享，可在線閱讀，更多相關(guān)《安徽省2022中考數(shù)學(xué)決勝二輪復(fù)習(xí) 專題三 圖表信息問題習(xí)題（4頁珍藏版）》請在裝配圖網(wǎng)上搜索。

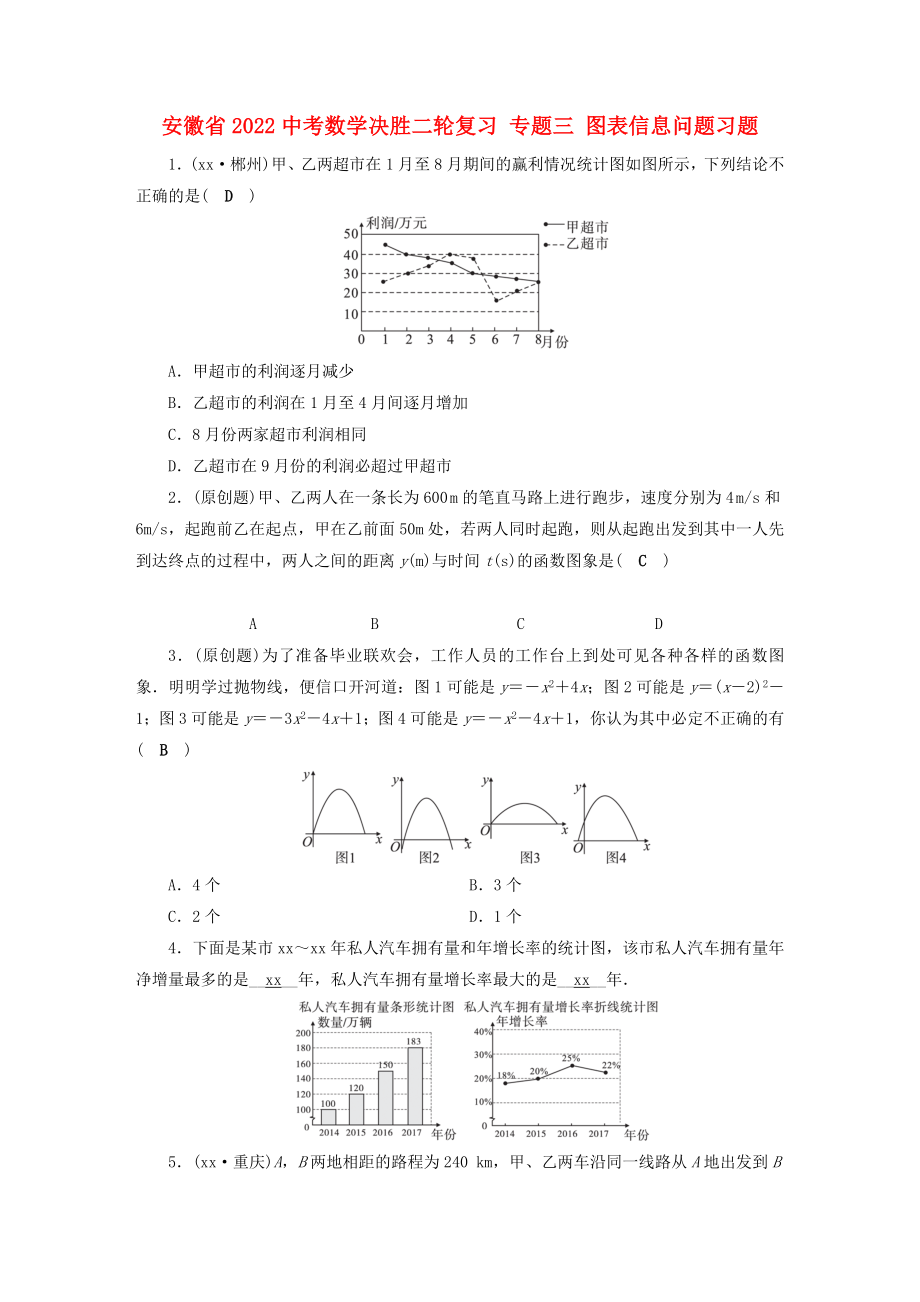
1、安徽省2022中考數(shù)學(xué)決勝二輪復(fù)習(xí) 專題三 圖表信息問題習(xí)題 1．(xx·郴州)甲、乙兩超市在1月至8月期間的贏利情況統(tǒng)計圖如圖所示，下列結(jié)論不正確的是(　D　) A．甲超市的利潤逐月減少 B．乙超市的利潤在1月至4月間逐月增加 C．8月份兩家超市利潤相同 D．乙超市在9月份的利潤必超過甲超市 2．(原創(chuàng)題)甲、乙兩人在一條長為600 m的筆直馬路上進行跑步，速度分別為4 m/s和6 m/s，起跑前乙在起點，甲在乙前面50 m處，若兩人同時起跑，則從起跑出發(fā)到其中一人先到達終點的過程中，兩人之間的距離y(m)與時間t(s)的函數(shù)圖象是(　C　) 　　　　　　 　　　　　A

2、 　　　　　　B　　　　　　 　　C　　　　　　　　D 3．(原創(chuàng)題)為了準(zhǔn)備畢業(yè)聯(lián)歡會，工作人員的工作臺上到處可見各種各樣的函數(shù)圖象．明明學(xué)過拋物線，便信口開河道：圖1可能是y＝－x2＋4x；圖2可能是y＝(x－2)2－1；圖3可能是y＝－3x2－4x＋1；圖4可能是y＝－x2－4x＋1，你認(rèn)為其中必定不正確的有(　B　) A．4個 B．3個 C．2個 D．1個 4．下面是某市xx～xx年私人汽車擁有量和年增長率的統(tǒng)計圖，該市私人汽車擁有量年凈增量最多的是__xx__年，私人汽車擁有量增長率最大的是__xx__年． 5．(xx·重慶)A，B兩地相距的路程為240 km

3、，甲、乙兩車沿同一線路從A地出發(fā)到B地，分別以一定的速度勻速行駛．甲車先出發(fā)40 min后，乙車才出發(fā)．途中乙車發(fā)生故障，修車耗時20 min，隨后，乙車車速比發(fā)生故障前減少了10 km/h(仍保持勻速前行)，甲、乙兩車同時到達B地．甲、乙兩車相離的路程y(km)與甲車行駛時間x(h)之間的函數(shù)關(guān)系如圖所示，求乙車修好時，甲車距B地還有__90__千米． 6．(原創(chuàng)題)如圖(1)所示，E為矩形ABCD的邊AD上一點，動點P，Q同時從點B出發(fā)，點P沿折線BE-ED-DC運動到點C時停止，點Q沿BC運動到點C時停止，它們運動的速度都是1 cm/s.設(shè)P，Q同時出發(fā)t秒時，△BPQ的面積為y

4、cm2.已知y與t的函數(shù)關(guān)系、圖象如圖(2)(曲線OM為拋物線的一部分)．則下列結(jié)論： ①AD＝BE＝5 cm；②cos∠ABE＝；③當(dāng)0＜t≤5時，y＝t2；④當(dāng)t＝秒時，△ABE∽△QBP.其中正確的有__①③④__(填序號) 7．(xx·襄陽)“品中華詩詞，尋文化基因”．某校舉辦了第二屆“中華詩詞大賽”，將該校八年級參加競賽的學(xué)生成績統(tǒng)計后，繪制了如下不完整的頻數(shù)分布統(tǒng)計表與頻數(shù)分布直方圖． 頻數(shù)分布統(tǒng)計表 組別 成績x(分) 人數(shù)(人) 百分比 A 60≤x<70 8 20% B 70≤x<80 16 m% C 80≤x<90 a 30% D

5、 90≤x≤100 4 10% (1)表中a＝__12__；m＝__40__； (2)補全頻數(shù)分布直方圖； (3)D組的4名學(xué)生中，有1名男生和3名女生．現(xiàn)從中隨機抽取2名學(xué)生參加市級競賽，則抽取的2名學(xué)生恰好是一名男生和一名女生的概率為____. 解：(1)a＝12，m＝40，理由如下：∵總?cè)藬?shù)為＝40(人)，∴C組人數(shù)為40×30%＝12(人)．∵B組百分比為1－20%－30%－10%＝40%，∴m＝40； (2)補全條形圖如下： (3)列表如下： 男 女1 女2 女3 男 … (女，男) (女，男) (女，男) 女1 (男，女) … (

6、女，女) (女，女) 女2 (男，女) (女，女) … (女，女) 女3 (男，女) (女，女) (女，女) … ∵共有12種等可能的結(jié)果，選中1名男生和1名女生結(jié)果的有6種．∴恰好選1名男生和1名女生的概率為＝. 8．(xx·錦州)某商場銷售一種商品，進價為每個20元，規(guī)定每個商品售價不低于進價，且不高于60元，經(jīng)調(diào)查發(fā)現(xiàn)，每天的銷售量y(個)與每個商品的售價x(元)滿足一次函數(shù)關(guān)系，其部分?jǐn)?shù)據(jù)如下所示. 每個商品的售價x(元) … 30 40 50 … 每天的銷售量y(個) … 100 80 60 … (1)求y與x之間的函數(shù)表達式；

7、(2)設(shè)商場每天獲得的總利潤為w(元)，求w與x之間的函數(shù)表達式； (3)不考慮其他因素，當(dāng)商品的售價為多少元時，商場每天獲得的總利潤最大，最大利潤是多少？ 解：(1)設(shè)y與x之間的函數(shù)解析式為y＝kx＋b，則解得即y與x之間的函數(shù)表達式是y＝－2x＋160； (2)由題意可得w＝(x－20)(－2x＋160)＝－2x2＋200x－3 200，即w與x之間的函數(shù)表達式是w＝－2x2＋200x－3 200； (3)∵w＝－2x2＋200x－3 200＝－2(x－50)2＋1 800，20≤x≤60，∴當(dāng)20≤x≤50時，w隨x的增大而增大；當(dāng)50≤x≤60時，w隨x的增大而減??；當(dāng)x＝5

8、0時，w取得最大值，此時w＝1 800.即當(dāng)商品的售價為50元時，商場每天獲得的總利潤最大，最大利潤是1 800. 9．(改編題)如圖，甲、丙兩地相距500 km，一列快車從甲地駛往丙地，且途中經(jīng)過乙地；一列慢車從乙地駛往丙地，兩車同時出發(fā)同向而行，設(shè)慢車行駛的時間為x(h)，兩車之間的距離為y(km)，圖中的折線表示y與x之間的函數(shù)關(guān)系．根據(jù)圖象進行以下探究． (1)求甲、乙兩地之間的距離； (2)求慢車和快車的速度； (3)求線段CD所表示的y與x之間的函數(shù)關(guān)系式，并寫出自變量x的取值范圍； (4)若這列快車從甲地駛往丙地，慢車從丙地駛往甲地，兩車同時出發(fā)相向而行，且兩車

9、的車速各自不變．設(shè)慢車行駛的時間為x(h)，兩車之間的距離為y(km)，則下列四個圖象中，哪一圖象中的折線能表示此時y(km)和時間x(h)之間的函數(shù)關(guān)系，請寫出你認(rèn)為可能合理的代號，并直接寫出折線中拐點A，B，C或A，B，C，D的坐標(biāo)． 解：(1)∵點A(0,150)，∴甲乙兩地之間的距離為150 km； (2)慢車速度：(500－150)÷3.5＝100(km/h)；快車速度：150＋100＝250(km/h)； (3)500÷250＝2(h)，350－100×2＝150(km)，∴點C坐標(biāo)為(2,150)，設(shè)yCD＝kx＋b，把點C(2,150)，D(3.5，0)代入得解得∴yCD＝－100x＋350(2≤x≤3.5)； (4)由分析可知，圖象(c)中的折線能表示此時y(km)和時間x(h)之間的函數(shù)關(guān)系，A(0,500)，B，C(2,150)，D(5,500)．