《【解題決策】2021屆中考數(shù)學(xué)總復(fù)習(xí) 課時39 與圓有關(guān)的計(jì)算熱身訓(xùn)練(無答案)》由會員分享���,可在線閱讀����,更多相關(guān)《【解題決策】2021屆中考數(shù)學(xué)總復(fù)習(xí) 課時39 與圓有關(guān)的計(jì)算熱身訓(xùn)練(無答案)(3頁珍藏版)》請?jiān)谘b配圖網(wǎng)上搜索�。
1�、
課時39.與圓有關(guān)的計(jì)算
【課前熱身】
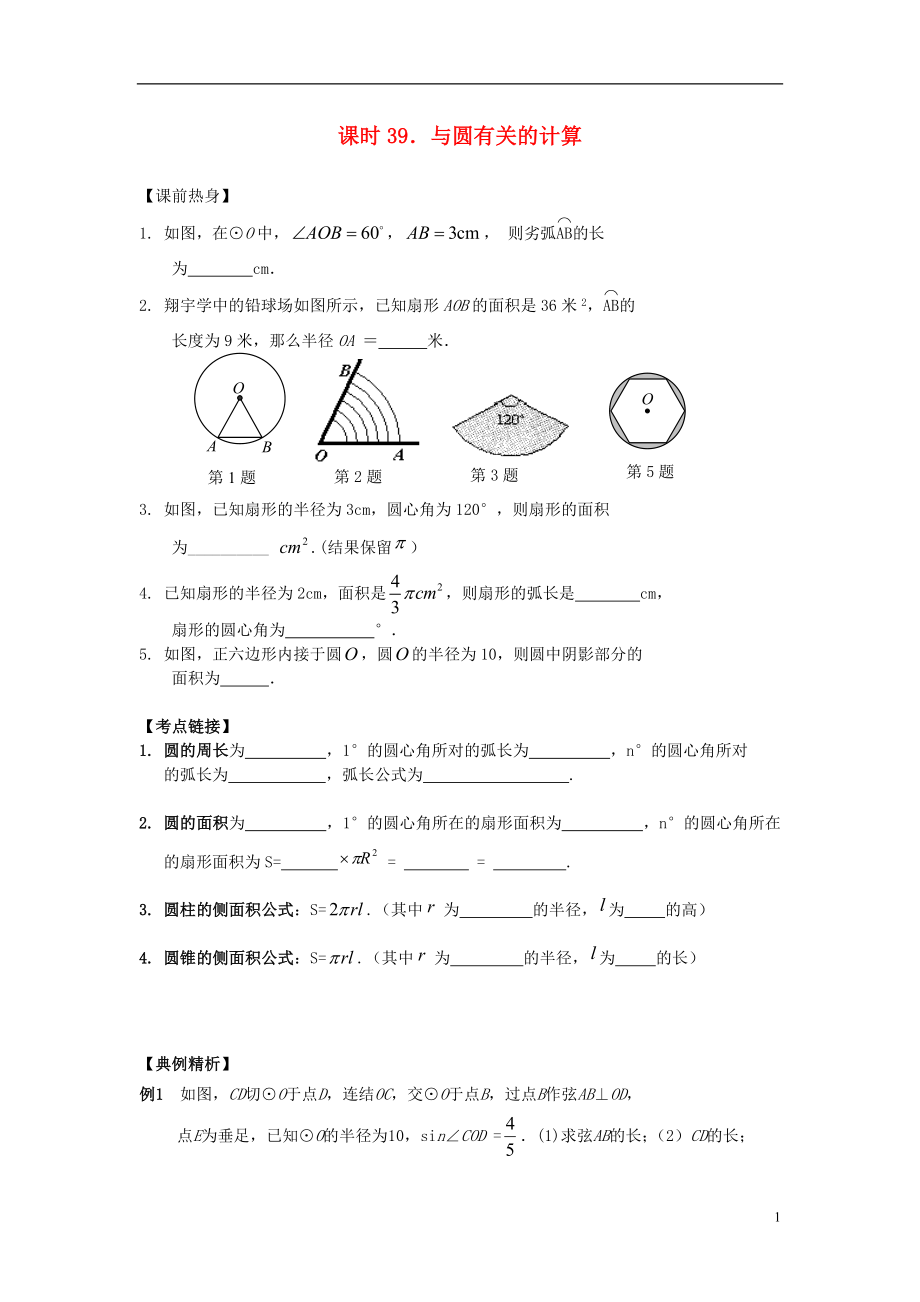
1. 如圖,在⊙O中���,��,��, 則劣弧的長
為 cm.
2. 翔宇學(xué)中的鉛球場如圖所示���,已知扇形AOB的面積是36米2,的
長度為9米�,那么半徑OA = 米.
O
第5題
第2題
第1題
A
B
O
第3題
3. 如圖,已知扇形的半徑為3cm��,圓心角為120°,則扇形的面積
為���������������������__________ .(結(jié)果保留)
4. 已知扇形的半徑為2cm���,面積是�����,則扇形的弧長是 cm��,
扇形的圓心角為 °.
2����、
5. 如圖��,正六邊形內(nèi)接于圓���,圓的半徑為10�����,則圓中陰影部分的
面積為 .
【考點(diǎn)鏈接】
1. 圓的周長為 ���,1°的圓心角所對的弧長為 ,n°的圓心角所對
的弧長為 ��,弧長公式為 .
2. 圓的面積為 ,1°的圓心角所在的扇形面積為 ���,n°的圓心角所在的扇形面積為S= = = .
3. 圓柱的側(cè)面積公式:S=.(其中為 的半徑�,為 的高)
4. 圓錐的側(cè)面積公
3�����、式:S=.(其中為 的半徑����,為 的長)
【典例精析】
例1 如圖���,CD切⊙O于點(diǎn)D�,連結(jié)OC���,交⊙O于點(diǎn)B�,過點(diǎn)B作弦AB⊥OD�����,
點(diǎn)E為垂足����,已知⊙O的半徑為10�,sin∠COD =.(1)求弦AB的長�;(2)CD的長;
(3)劣弧AB的長.(結(jié)果保留三個有效數(shù)字�,,≈3.142)
例2 如圖�����,為⊙O的直徑����,于點(diǎn),交⊙O于點(diǎn)��,
于點(diǎn).
(1)請寫出三條與有關(guān)的正確結(jié)論��;
C
B
A
O
F
D
E
(2)當(dāng)���,時��,求圓中陰影部分的面積.
例3 如圖��,線段與⊙O相切于點(diǎn)�����,連結(jié)
4��、�����、��,交⊙O于點(diǎn)D��,已知����,.
求(1)⊙O的半徑�; (2)圖中陰影部分的面積.
D
【中考演練】
1. 中,����,,���,兩等圓⊙A����,⊙B外切,那么圖中兩個扇形(即陰影部分)的面積之和為( )
A. B. C. D.
2. 如圖��,在矩形空地上鋪4塊扇形草地.若扇形的半徑均為米����,圓心角均為,則鋪上的草地共有 平方米.
A
B
C
3. 如圖����,已知是⊙O的直徑,點(diǎn)在⊙O上��,且�,.
(1)求的值;
A
B
C
D
O
(2)如果���,垂足為�,求的長�����;
(3)求圖中陰影部分的面積(精確到0.1).
﹡4. 如圖,從一個直徑是2的圓形鐵皮中剪下一個圓心角為的扇形.
(1)求這個扇形的面積(結(jié)果保留)����;
(2)在剩下的三塊余料中,能否從第③塊余料中剪出一個圓作為底面與此扇形圍成一個圓錐�����?請說明理由.
①
②
③
(3)當(dāng)⊙O的半徑為任意值時����,(2)中的結(jié)論是否仍然成立?請說明理由.
3
 【解題決策】2021屆中考數(shù)學(xué)總復(fù)習(xí) 課時39 與圓有關(guān)的計(jì)算熱身訓(xùn)練(無答案)
【解題決策】2021屆中考數(shù)學(xué)總復(fù)習(xí) 課時39 與圓有關(guān)的計(jì)算熱身訓(xùn)練(無答案)