《創(chuàng)新方案高考人教版數(shù)學(xué)理總復(fù)習(xí)練習(xí):第七章 立體幾何 課時(shí)作業(yè)42 Word版含解析》由會(huì)員分享�,可在線閱讀��,更多相關(guān)《創(chuàng)新方案高考人教版數(shù)學(xué)理總復(fù)習(xí)練習(xí):第七章 立體幾何 課時(shí)作業(yè)42 Word版含解析(17頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索��。
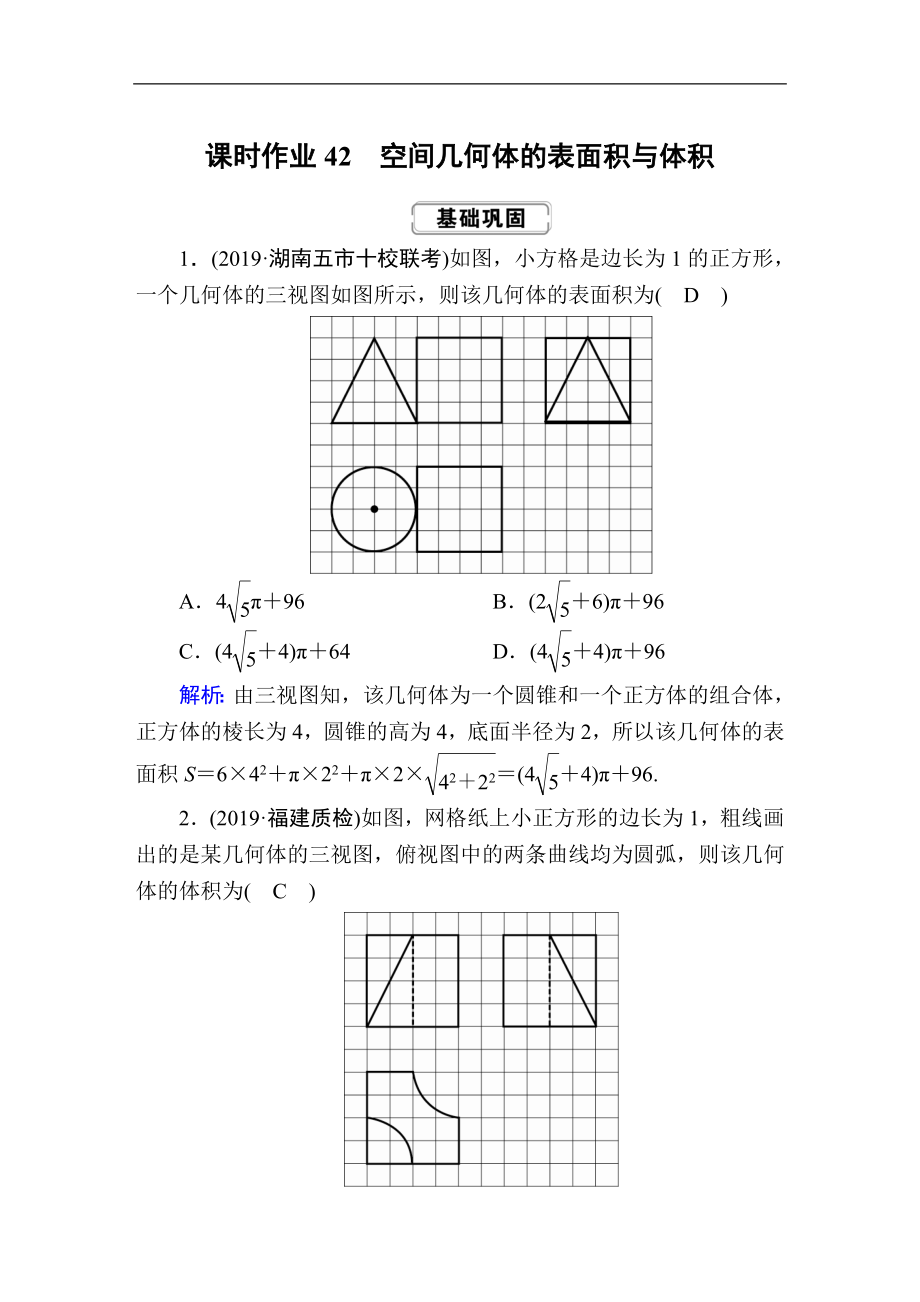
1�����、課時(shí)作業(yè)42空間幾何體的表面積與體積1(2019湖南五市十校聯(lián)考)如圖����,小方格是邊長(zhǎng)為1的正方形�,一個(gè)幾何體的三視圖如圖所示,則該幾何體的表面積為(D)A496 B(26)96C(44)64 D(44)96解析:由三視圖知�����,該幾何體為一個(gè)圓錐和一個(gè)正方體的組合體�����,正方體的棱長(zhǎng)為4��,圓錐的高為4�,底面半徑為2,所以該幾何體的表面積S642222(44)96.2(2019福建質(zhì)檢)如圖,網(wǎng)格紙上小正方形的邊長(zhǎng)為1���,粗線畫(huà)出的是某幾何體的三視圖��,俯視圖中的兩條曲線均為圓弧�����,則該幾何體的體積為(C)A64 B648C64 D64解析:由三視圖可知該幾何體是由棱長(zhǎng)為4的正方體截去個(gè)圓錐和個(gè)圓柱所得到的�,
2��、且圓錐的底面半徑為2����,高為4,圓柱的底面半徑為2����,高為4�����,所以該幾何體的體積為4364.故選C.3(2015全國(guó)卷)已知A�,B是球O的球面上兩點(diǎn),AOB90�����,C為該球面上的動(dòng)點(diǎn)若三棱錐O-ABC體積的最大值為36,則球O的表面積為(C)A36 B64C144 D256解析:SOAB是定值�����,且VO-ABCVC-OAB���,當(dāng)OC平面OAB時(shí)����,VC-OAB最大�,即VO-ABC最大設(shè)球O的半徑為R,則(VO-ABC)maxR2RR336�,R6,球O的表面積S4R2462144.4(2019河南濮陽(yáng)一模)已知三棱錐A-BCD中��,ABD與BCD是邊長(zhǎng)為2的等邊三角形且二面角A-BD-C為直二面角��,則三棱錐A
3�����、-BCD的外接球的表面積為(D)A. B5C6 D.解析:如圖,取BD中點(diǎn)M���,連接AM��,CM�����,取ABD���,CBD的中心即AM,CM的三等分點(diǎn)P�,Q,過(guò)P作平面ABD的垂線�,過(guò)Q作平面CBD的垂線,兩垂線相交于點(diǎn)O��,則點(diǎn)O為外接球的球心����,如圖,其中OQ���,CQ,連接OC,則外接球的半徑ROC����,表面積為4R2,故選D.5一個(gè)多面體的直觀圖和三視圖如圖所示����,點(diǎn)M是AB上的動(dòng)點(diǎn),記四面體EFMC的體積為V1��,多面體ADF-BCE的體積為V2�,則(B)A. B.C. D.解析:由三視圖可知多面體ADF-BCE是直三棱柱,其底面是等腰直角三角形(直角邊長(zhǎng)為a)���,且四邊形DFEC與四邊形ABCD都是正方形����,它們
4�、的邊長(zhǎng)均為a.M是AB上的動(dòng)點(diǎn),且易知AB平面DFEC�����,點(diǎn)M到平面DFEC的距離等于點(diǎn)B到平面DFEC的距離�����,距離為a,V1VE-FMCVM-EFCaaa�����,又V2aaa�,故.6某工件的三視圖如圖所示,現(xiàn)將該工件通過(guò)切削��,加工成一個(gè)體積盡可能大的長(zhǎng)方體新工件��,并使新工件的一個(gè)面落在原工件的一個(gè)面內(nèi)���,則原工件材料的利用率為(A)A. B.C. D.解析:原工件是一個(gè)底面半徑為1��,高為2的圓錐�,依題意加工后的新工件是圓錐的內(nèi)接長(zhǎng)方體�,且落在圓錐底面上的面是正方形,設(shè)正方形的邊長(zhǎng)為a����,長(zhǎng)方體的高為h,則0a��,0h2.于是,h2a.令f(a)V長(zhǎng)方體a2h2a2a3�����,f(a)4a3a2��,當(dāng)f(a)0時(shí)���,
5、a.易知f(a)maxf.材料利用率���,故選A.7(2017全國(guó)卷)如圖�����,網(wǎng)格紙上小正方形的邊長(zhǎng)為1����,粗實(shí)線畫(huà)出的是某幾何體的三視圖��,該幾何體由一平面將一圓柱截去一部分后所得���,則該幾何體的體積為(B)A90 B63C42 D36解析:由三視圖可知兩個(gè)同樣的幾何體可以拼成一個(gè)底面直徑為6��,高為14的圓柱�����,所以該幾何體的體積V321463����,故選B.8已知三棱錐O-ABC的頂點(diǎn)A,B��,C都在半徑為2的球面上��,O是球心��,AOB120��,當(dāng)AOC與BOC的面積之和最大時(shí)��,三棱錐O-ABC的體積為(B)A. B.C. D.解析:設(shè)球O的半徑為R�,因?yàn)镾AOCSBOCR2(sinAOCsinBOC),所以當(dāng)AO
6���、CBOC90時(shí)��,SAOCSBOC取得最大值���,此時(shí)OAOC�,OBOC�����,又OBOAO���,OA,OB平面AOB�����,所以O(shè)C平面AOB����,所以V三棱錐O-ABCV三棱錐C-OABOCOAOBsinAOBR3sinAOB,故選B.9某組合體的三視圖如圖所示��,則該組合體的體積為.解析:如圖所示��,該組合體由一個(gè)四棱錐和四分之一個(gè)球組成��,球的半徑為1����,四棱錐的高為球的半徑����,四棱錐的底面為等腰梯形���,上底為2�����,下底為1����,高為����,所以該組合體的體積V(21)113.10(2018全國(guó)卷)已知圓錐的頂點(diǎn)為S,母線SA����,SB互相垂直,SA與圓錐底面所成角為30.若SAB的面積為8�,則該圓錐的體積為8.解析:設(shè)圓錐底面半徑為r,
7、母線長(zhǎng)為l����,高為h,因?yàn)槟妇€SA與底面所成的角為30����,所以lr.由SAB的面積為8得l28,即r28���,所以r212�,hr2.所以圓錐的體積為r2h1228.11(2019江西南昌二中模擬)在三棱錐S-ABC中����,ABC是邊長(zhǎng)為3的等邊三角形���,SA�,SB2���,二面角S-AB-C的大小為120�����,則此三棱錐的外接球的表面積為21.解析:根據(jù)題意得SA2AB2SB2�����,即SAAB.取AB的中點(diǎn)為D���,SB的中點(diǎn)為M����,連接CD�、MD,得CDM為二面角S-AB-C的平面角�,MDC120.如圖,設(shè)三角形ABC的外心為O1�,則O1在CD上,連接BO1��,則CO1BO1���,DO1.設(shè)外接球半徑為R���,易知球心為過(guò)M垂直面AB
8、S的垂線與過(guò)O1垂直面ABC的垂線的交點(diǎn)O.在四邊形MDO1O中��,二面角S-AB-C的平面角MDC120,且MOMD�����,O1ODO1��,MDO1D�,ODO160,OO1O1Dtan60���,連接OB����,R2OB2OOO1B23��,球的表面積S4R221.12如圖��,四棱錐P-ABCD中��,側(cè)面PAD為等邊三角形且垂直于底面ABCD���,ABBCAD,BADABC90.(1)證明:直線BC平面PAD�����;(2)若PCD的面積為2,求四棱錐P-ABCD的體積解:(1)證明:在平面ABCD內(nèi)���,因?yàn)锽ADABC90��,所以BCAD.又BC平面PAD�����,AD平面PAD�,故BC平面PAD.(2)取AD的中點(diǎn)M����,連接PM,CM.由AB
9��、BCAD及BCAD��,ABC90得四邊形ABCM為正方形�,則CMAD.因?yàn)閭?cè)面PAD為等邊三角形且垂直于底面ABCD,平面PAD平面ABCDAD��,所以PMAD��,PM底面ABCD.因?yàn)镃M底面ABCD,所以PMCM.設(shè)BCx�,則CMx,CDx���,PMx�,PCPD2x.取CD的中點(diǎn)N����,連接PN,則PNCD��,所以PNx.因?yàn)镻CD的面積為2����,所以xx2,解得x2(舍去)或x2.于是ABBC2�,AD4,PM2.所以四棱錐P-ABCD的體積V24.13九章算術(shù)是我國(guó)古代內(nèi)容極為豐富的數(shù)學(xué)名著��,書(shū)中有如下問(wèn)題:“今有芻甍�,下廣三丈���,袤四丈����;上袤二丈,無(wú)廣��;高一丈�����,問(wèn):積幾何�?”其意思為:“今有底面為矩形的屋脊
10、柱的楔體�����,下底面寬3丈����,長(zhǎng)4丈;上棱長(zhǎng)2丈����,高一丈,問(wèn)它的體積是多少�?”已知1丈為10尺,現(xiàn)將該楔體的三視圖給出���,其中網(wǎng)格紙上小正方形的邊長(zhǎng)為1丈��,則該楔體的體積為(A)A5 000立方尺 B5 500立方尺C6 000立方尺 D6 500立方尺解析:該楔體的直觀圖如圖中的幾何體ABCDEF.取AB的中點(diǎn)G�,CD的中點(diǎn)H,連接FG�,GH,HF�,則該幾何體的體積為四棱錐F-GBCH與三棱柱ADE-GHF的體積之和又可以將三棱柱ADE-GHF割補(bǔ)成高為EF,底面積為S31平方丈的一個(gè)直棱柱��,故該楔體的體積V22315立方丈5 000立方尺14(2019深圳調(diào)研)如圖所示��,在平面四邊形ABCD中����,A
11、BADCD1���,BD���,BDCD,將其沿對(duì)角線BD折成四面體ABCD�����,使平面ABD平面BCD�����,若四面體ABCD的頂點(diǎn)在同一個(gè)球面上��,則該球的體積為(A)A. B3 C. D2解析:如圖�����,取BD的中點(diǎn)為E����,BC的中點(diǎn)為O,連接AE�,OD,EO���,AO.因?yàn)锳BAD����,所以AEBD.由于平面ABD平面BCD�����,所以AE平面BCD.因?yàn)锳BADCD1,BD�,所以AE,EO.所以O(shè)A.在RtBDC中��,OBOCODBC���,所以四面體ABCD的外接球的球心為O�����,半徑為.所以該球的體積V3.15(2017全國(guó)卷)如圖��,圓形紙片的圓心為O����,半徑為5 cm�,該紙片上的等邊三角形ABC的中心為O.D,E����,F(xiàn)為圓O上的點(diǎn),DB
12����、C����,ECA��,F(xiàn)AB分別是以BC���,CA,AB為底邊的等腰三角形沿虛線剪開(kāi)后���,分別以BC����,CA����,AB為折痕折起DBC,ECA���,F(xiàn)AB���,使得D,E,F(xiàn)重合�����,得到三棱錐當(dāng)ABC的邊長(zhǎng)變化時(shí)��,所得三棱錐體積(單位:cm3)的最大值為4.解析:解法一:由題意可知��,折起后所得三棱錐為正三棱錐����,設(shè)ABC的邊長(zhǎng)為a(a0)cm,則ABC的面積為a2 cm2����,點(diǎn)O到ABC三邊的距離都為a cm,DBC的高為cm�,則正三棱錐的高為 cm,25a0��,0a5��,所得三棱錐的體積Va2 cm3.令t25a4a5�,則t100a3a4,由t0�,得a4(滿足0a5)����,易知此時(shí)所得三棱錐的體積最大����,為4 cm3.解法二:由題意知折
13、起以后所得三棱錐的直觀圖如圖所示��,連接CO并延長(zhǎng)交AB于H�����,連接DO��、DH.則DO平面ABC.令OHx cm���,則OC2x cm,DH(5x) cm�,得OD cm,AB2x cm.則VD-ABCx2x2 cm3�,令f(x)x2,則f(x)��,則當(dāng)x(0,2)時(shí)���,f(x)單調(diào)遞增�,當(dāng)x(2,2.5)時(shí),f(x)單調(diào)遞減��,所以當(dāng)x2時(shí)�����,體積取最大值��,為44 cm3.16(2019貴陽(yáng)質(zhì)檢)如圖�,ABC內(nèi)接于圓O,AB是圓O的直徑���,四邊形DCBE為平行四邊形���,DC平面ABC,AB2�����,EB.(1)求證:DE平面ACD�����;(2)設(shè)ACx,V(x)表示三棱錐B-ACE的體積���,求函數(shù)V(x)的解析式及最大值解:(1)證明:四邊形DCBE為平行四邊形��,CDBE��,BCDE.DC平面ABC����,BC平面ABC�����,DCBC.AB是圓O的直徑�,BCAC����,且DCACC,DC����,AC平面ADC,BC平面ADC.DEBC�,DE平面ADC.(2)DC平面ABC��,BE平面ABC.在RtABE中�����,AB2��,EB.在RtABC中�,ACx���,BC(0x2)�����,SABCACBCx�����,V(x)V三棱錐E-ABCx(0x2)x2(4x2)24�����,當(dāng)且僅當(dāng)x24x2�����,即x時(shí)取等號(hào)��,當(dāng)x時(shí)��,體積有最大值.
 創(chuàng)新方案高考人教版數(shù)學(xué)理總復(fù)習(xí)練習(xí):第七章 立體幾何 課時(shí)作業(yè)42 Word版含解析
創(chuàng)新方案高考人教版數(shù)學(xué)理總復(fù)習(xí)練習(xí):第七章 立體幾何 課時(shí)作業(yè)42 Word版含解析