《安徽省迎河中學(xué)2014年度高三期終教學(xué)質(zhì)量檢測 理科數(shù)學(xué)試題》由會員分享��,可在線閱讀�����,更多相關(guān)《安徽省迎河中學(xué)2014年度高三期終教學(xué)質(zhì)量檢測 理科數(shù)學(xué)試題(6頁珍藏版)》請在裝配圖網(wǎng)上搜索����。
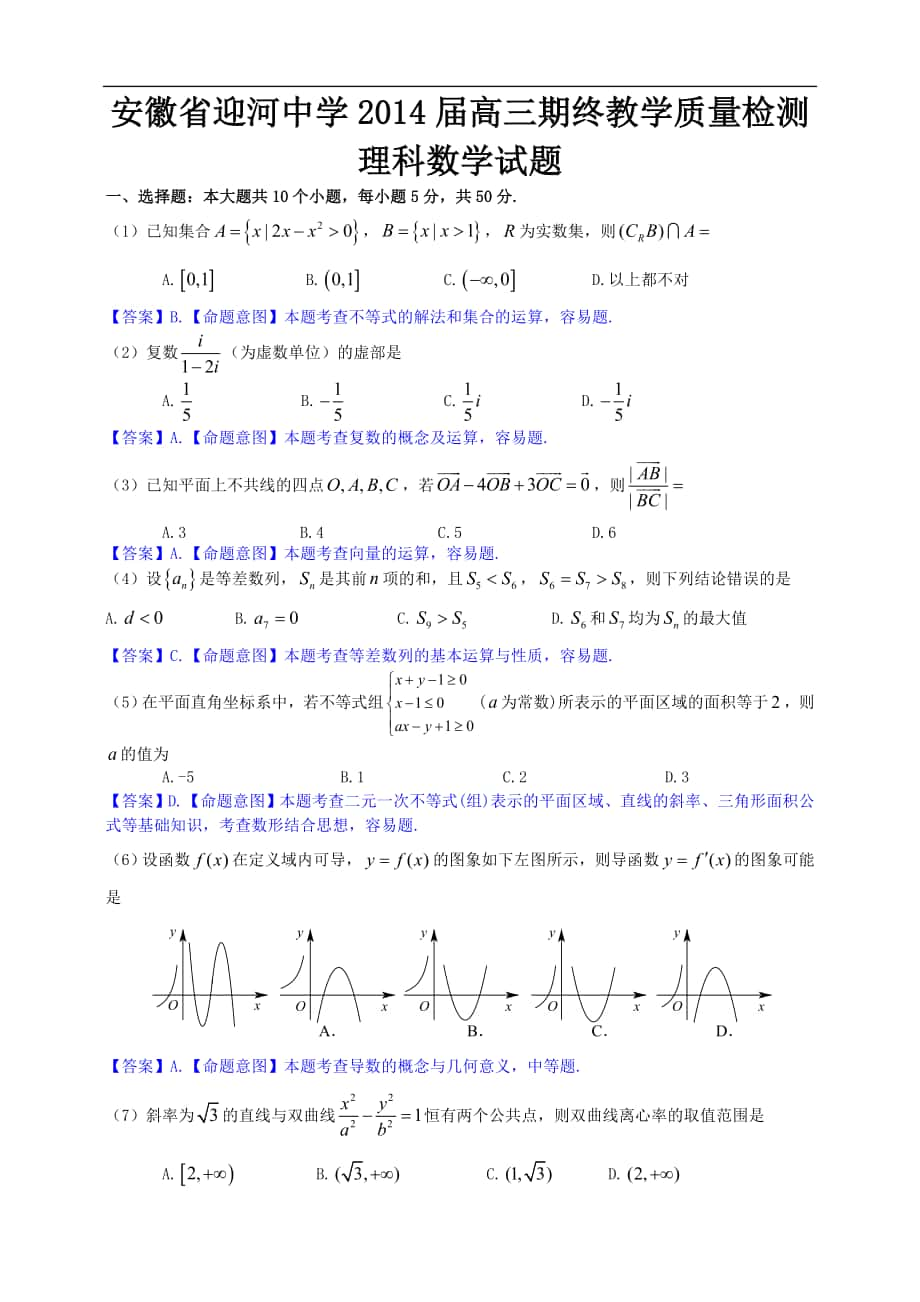
1、安徽省迎河中學(xué)2014屆高三期終教學(xué)質(zhì)量檢測理科數(shù)學(xué)試題一����、選擇題:本大題共10個小題,每小題5分�����,共50分.(1)已知集合���,為實(shí)數(shù)集�����,則A. B. C. D.以上都不對【答案】B.【命題意圖】本題考查不等式的解法和集合的運(yùn)算���,容易題.(2)復(fù)數(shù)(為虛數(shù)單位)的虛部是A. B. C. D.【答案】A.【命題意圖】本題考查復(fù)數(shù)的概念及運(yùn)算�,容易題.(3)已知平面上不共線的四點(diǎn)�����,若���,則A.3 B.4 C.5 D.6【答案】A.【命題意圖】本題考查向量的運(yùn)算����,容易題.(4)設(shè)是等差數(shù)列���,是其前項(xiàng)的和�����,且�,則下列結(jié)論錯誤的是A. B. C. D.和均為的最大值【答案】C.【命題意圖】本題考查等差數(shù)列的
2�����、基本運(yùn)算與性質(zhì)�,容易題.(5)在平面直角坐標(biāo)系中,若不等式組(為常數(shù))所表示的平面區(qū)域的面積等于�����,則的值為A.-5 B.1 C.2 D.3 【答案】D.【命題意圖】本題考查二元一次不等式(組)表示的平面區(qū)域��、直線的斜率��、三角形面積公式等基礎(chǔ)知識�����,考查數(shù)形結(jié)合思想�,容易題.(6)設(shè)函數(shù)在定義域內(nèi)可導(dǎo),的圖象如下左圖所示����,則導(dǎo)函數(shù)的圖象可能是A B C D【答案】A.【命題意圖】本題考查導(dǎo)數(shù)的概念與幾何意義,中等題.(7)斜率為的直線與雙曲線恒有兩個公共點(diǎn)���,則雙曲線離心率的取值范圍是A. B. C. D.【答案】D.【命題意圖】本題考查雙曲線的性質(zhì)��,中等題.(8)已知一個棱長為的正方體����,被一個平面
3、截后所得幾何體的三視圖如圖所示��,則該幾何體的體積是A.8 B. C. D.【答案】C.【命題意圖】本題考查三視圖的概念與幾何體體積的計算�����,考查空間想象能力��,較難題.(9)袋中有大小相同的個紅球和個白球��,隨機(jī)從袋中取個球��,取后不放回�,那么恰好在第次取完紅球的概率是A. B. C. D.【答案】B.【命題意圖】本題考查排列組合、古典概型等基礎(chǔ)知識����,考查分析問題解決問題的能力,較難題.(10)已知函數(shù)是以為周期的偶函數(shù)���,當(dāng)時��,若關(guān)于的方程()在區(qū)間內(nèi)有四個不同的實(shí)根�,則的取值范圍是A. B. C. D.【答案】C.【命題意圖】本題考查函數(shù)的性質(zhì)與圖象,考查數(shù)形結(jié)合能力����,較難題.二�����、填空題:本大題共5
4�����、個小題�����,每小題5分�����,共25分請在答題卡上答題(11)運(yùn)行如圖所示的程序框圖��,若輸入��,則輸出的值為 . 【答案】11.【命題意圖】本題考查程序框圖��,容易題.(12)已知總體的各個個體的值由小到大依次為,且總體的中位數(shù)為��,若要使該總體的標(biāo)準(zhǔn)差最小��,則 .【答案】12.【命題意圖】本題考查統(tǒng)計知識����,重要不等式,容易題.說明:本題數(shù)據(jù)給的不科學(xué)�,改為較好(13)已知的展開式中第三項(xiàng)與第五項(xiàng)的系數(shù)之比為,則展開式中常數(shù)項(xiàng)是_【答案】45.【命題意圖】本題考查二項(xiàng)式定理���,考查運(yùn)算能力����,中等題.(14)已知直線(是實(shí)數(shù))與圓相交于兩點(diǎn)����,且(是坐標(biāo)原點(diǎn))是直角三角形,則點(diǎn)與點(diǎn)之間距離的最小值是 .【答案】.【
5���、命題意圖】本題考查直線與圓的方程���,考查運(yùn)算能力與數(shù)形結(jié)合能力�����,中等題.(15)函數(shù)的圖象為�,如下結(jié)論中正確的是(寫出所有正確結(jié)論的編號)圖象關(guān)于直線對稱��; 圖象的所有對稱中心都可以表示為��;函數(shù)在區(qū)間內(nèi)是增函數(shù)��;由的圖象向左平移個單位長度可以得到圖象函數(shù)在上的最小值是.【答案】. 【命題意圖】本題考查三角函數(shù)的圖象與性質(zhì)��,較難題.三��、解答題:本大題共6個小題����,滿分75分.解答應(yīng)寫出必要的文字說明���、證明過程或演算步驟.(16)(本題滿分12分) 在中����,分別是角的對邊����,.()求的值�����;()若���,求邊的長.(16)【命題意圖】本題考查兩角和與差的三角函數(shù)、平面向量的數(shù)量積定義�����、正弦定理�����、余弦定理等基礎(chǔ)知識
6�����、����,考查邏輯推理和運(yùn)算求解能力,簡單題解:()����,. ���, .6分(),�����;又由正弦定理�,得,解得�,即邊的長為5.12分(17)(本題滿分12分)一廠家向用戶提供的一箱產(chǎn)品共10件�,其中有件次品,用戶先對產(chǎn)品進(jìn)行抽檢以決定是否接收抽檢規(guī)則是這樣的:一次取一件產(chǎn)品檢查(取出的產(chǎn)品不放回箱子)�����,若前三次沒有抽查到次品�����,則用戶接收這箱產(chǎn)品��;若前三次中一抽查到次品就立即停止抽檢���,并且用戶拒絕接收這箱產(chǎn)品.()求這箱產(chǎn)品被用戶接收的概率���;()記抽檢的產(chǎn)品件數(shù)為�,求隨機(jī)變量的分布列和數(shù)學(xué)期望(17)【命題意圖】本題考查概率知識�����,分布列和期望的求法��,考查學(xué)生應(yīng)用知識解決問題的能力�����,中等題.解:()設(shè)“這箱產(chǎn)品被用戶
7�、接收”為事件,則.即這箱產(chǎn)品被用戶接收的概率為4分()的可能取值為1���,2��,3 5分����, , 8分的概率分布列為:12310分 (12分)(18)(本題滿分12分)在如圖的多面體中���,平面����,,�,是的中點(diǎn)() 求證:平面;() 求證:���;() 求二面角的余弦值.(18)【命題意圖】本題考查線面位置關(guān)系�����、二面角等有關(guān)知識�,考查空間想象能力���,中等題.解:()證明:,����; 又,是的中點(diǎn)���,且���,四邊形是平行四邊形���, . 平面,平面�,平面. 4分() 解法1:證明:平面,平面�,;又�����,平面�,平面. 過作交于,則平面. 平面����, .,四邊形平行四邊形��,又����,四邊形為正方形, ,又平面�����,平面����,平面. 平面,. 8分解法2:平面
8����、,平面�����,平面��,又�,兩兩垂直. 以點(diǎn)為坐標(biāo)原點(diǎn),分別為軸建立如圖所示的空間直角坐標(biāo)系. 由已知得���,;����,�����。8分()由已知得是平面的法向量. 設(shè)平面的法向量為�����,即��,令,得. 設(shè)二面角的大小為�,由法向量與的方向可知�,即二面角的余弦值為.12分(19)(本題滿分12分)已知數(shù)列滿足.()證明數(shù)列是等差數(shù)列;()求數(shù)列的通項(xiàng)公式��;()設(shè)����,求數(shù)列的前項(xiàng)和.(19)【命題意圖】本題考查等差數(shù)列與等比數(shù)列的概念與通項(xiàng)公式、數(shù)列求和等基礎(chǔ)知識知識����,考查運(yùn)算求解能力、推理論證能力�,中等題.解:()由已知可得��,所以�,即���,數(shù)列是公差為1的等差數(shù)列.4分()由(1)可得�,.7分()由(2)知���,所以���,相減得 ,.12分(2
9��、0)(本題滿分13分)已知橢圓:()過點(diǎn)�����,其左����、右焦點(diǎn)分別為,且.()求橢圓的方程���;()若是直線上的兩個動點(diǎn)�����,且�����,則以為直徑的圓是否過定點(diǎn)����?請說明理由(20)【命題意圖】本題考查圓與橢圓的方程等相關(guān)知識���,考查運(yùn)算求解能力以及分析問題�����、解決問題的能力��,較難題.解:()設(shè)點(diǎn)的坐標(biāo)分別為���,則,故�����,可得,2分 所以��,4分���,所以橢圓的方程為6分()設(shè)的坐標(biāo)分別為����,則��,. 由�����,可得����,即, 8分又圓的圓心為半徑為�,故圓的方程為,即�����,也就是��,令,可得或���,故圓必過定點(diǎn)和13分(21)(本題滿分14分)設(shè)函數(shù),且為的極值點(diǎn)() 若為的極大值點(diǎn)�,求的單調(diào)區(qū)間(用表示);() 若恰有兩解�,求實(shí)數(shù)的取值范圍(21)【命題意圖】本題考查導(dǎo)數(shù)的應(yīng)用,分類討論思想���,考查運(yùn)算求解能力�、邏輯思維能力和分析問題解決問題的能力�����,較難題.解:�����,又�����,則�����,所以且, 3分()因?yàn)闉榈臉O大值點(diǎn)��,所以. 令���,得或��;令����,得. 所以的遞增區(qū)間為��,���;遞減區(qū)間為6分()若�����,則在上遞減�����,在上遞增. 若恰有兩解����,則,即��,所以. 若�,則,. 因?yàn)?��,則,從而只有一解��;若���,則��,從而�,則只有一解.綜上�����,使恰有兩解的的范圍為14分
 安徽省迎河中學(xué)2014年度高三期終教學(xué)質(zhì)量檢測 理科數(shù)學(xué)試題
安徽省迎河中學(xué)2014年度高三期終教學(xué)質(zhì)量檢測 理科數(shù)學(xué)試題