《2022年高考數(shù)學(xué)二輪復(fù)習(xí) 第1篇 專題7 解析幾何學(xué)案》由會員分享，可在線閱讀，更多相關(guān)《2022年高考數(shù)學(xué)二輪復(fù)習(xí) 第1篇 專題7 解析幾何學(xué)案（3頁珍藏版）》請在裝配圖網(wǎng)上搜索。
1、2022年高考數(shù)學(xué)二輪復(fù)習(xí) 第1篇 專題7 解析幾何學(xué)案
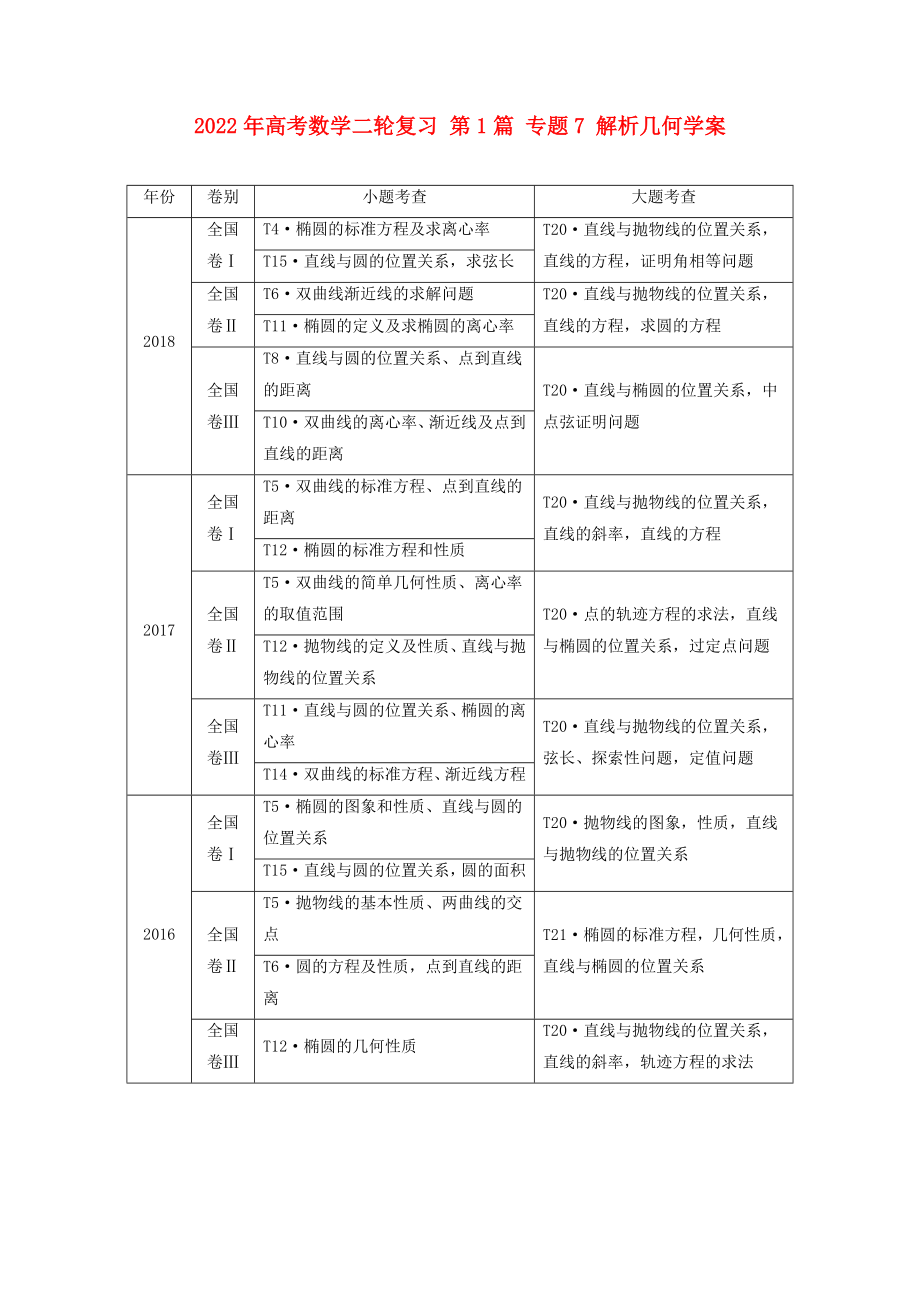
年份
卷別
小題考查
大題考查
2018
全國卷Ⅰ
T4·橢圓的標(biāo)準方程及求離心率
T20·直線與拋物線的位置關(guān)系，直線的方程，證明角相等問題
T15·直線與圓的位置關(guān)系，求弦長
全國卷Ⅱ
T6·雙曲線漸近線的求解問題
T20·直線與拋物線的位置關(guān)系，直線的方程，求圓的方程
T11·橢圓的定義及求橢圓的離心率
全國卷Ⅲ
T8·直線與圓的位置關(guān)系、點到直線的距離
T20·直線與橢圓的位置關(guān)系，中點弦證明問題
T10·雙曲線的離心率、漸近線及點到直線的距離
2017
全國卷Ⅰ
T5·雙曲線的標(biāo)準方
2、程、點到直線的距離
T20·直線與拋物線的位置關(guān)系，直線的斜率，直線的方程
T12·橢圓的標(biāo)準方程和性質(zhì)
全國卷Ⅱ
T5·雙曲線的簡單幾何性質(zhì)、離心率的取值范圍
T20·點的軌跡方程的求法，直線與橢圓的位置關(guān)系，過定點問題
T12·拋物線的定義及性質(zhì)、直線與拋物線的位置關(guān)系
全國卷Ⅲ
T11·直線與圓的位置關(guān)系、橢圓的離心率
T20·直線與拋物線的位置關(guān)系，弦長、探索性問題，定值問題
T14·雙曲線的標(biāo)準方程、漸近線方程
2016
全國卷Ⅰ
T5·橢圓的圖象和性質(zhì)、直線與圓的位置關(guān)系
T20·拋物線的圖象，性質(zhì)，直線與拋物線的位置關(guān)系
T15·直線與圓的位置關(guān)系，
3、圓的面積
全國卷Ⅱ
T5·拋物線的基本性質(zhì)、兩曲線的交點
T21·橢圓的標(biāo)準方程，幾何性質(zhì)，直線與橢圓的位置關(guān)系
T6·圓的方程及性質(zhì)，點到直線的距離
全國卷Ⅲ
T12·橢圓的幾何性質(zhì)
T20·直線與拋物線的位置關(guān)系，直線的斜率，軌跡方程的求法
解析幾何問題重在“設(shè)”——設(shè)點、設(shè)線
解析幾何部分知識點多，運算量大，能力要求高，綜合性強，在高考試題中大都是在壓軸題的位置出現(xiàn)，是考生“未考先怕”的題型之一，不是怕解題無思路，而是怕解題過程中繁雜的運算．因此，在遵循“設(shè)——列——解”程序化運算的基礎(chǔ)上，應(yīng)突出解析幾何“設(shè)”的重要性，以克服平時重思路方法、輕運算技巧的頑疾，突
4、破如何避繁就簡這一瓶頸．
【典例】 已知拋物線C：y2＝2x的焦點為F，平行于x軸的兩條直線l1，l2分別交C于A，B兩點，交C的準線于P，Q兩點．
(1)若F在線段AB上，R是PQ的中點，證明AR∥FQ；
(2)若△PQF的面積是△ABF的面積的兩倍，求AB中點的軌跡方程．
[解題示范] 由題設(shè)F．
設(shè)l1：y＝a，l2：y＝b，則ab≠0?，
且A，B，P，Q，R．
記過A，B兩點的直線為l，
則l的方程為2x－(a＋b)y＋ab＝0．
(1)證明：由于F在線段AB上，故1＋ab＝0．
設(shè)AR的斜率為k1，F(xiàn)Q的斜率為k2，則
k1＝＝＝＝＝－b＝＝k2．
5、
所以AR∥FQ．
(2)解：設(shè)l與x軸的交點為D(x1,0)?，
則S△ABF＝|b－a||FD|＝|b－a||x1－|，
S△PQF＝．
由題設(shè)可得2×|b－a||x1－|＝，
所以x1＝0(舍去)，x1＝1．
設(shè)滿足條件的AB的中點為E(x，y)?．
當(dāng)AB與x軸不垂直時，
由kAB＝kDE可得＝(x≠1)．
而＝y(tǒng)，所以y2＝x－1(x≠1)．
當(dāng)AB與x軸垂直時，E與D重合，此時E(1,0)滿足方程y2＝x－1．
所以所求軌跡方程為y2＝x－1．
?設(shè)線：設(shè)出直線l1，l2可表示出點A，B，P，Q，R的坐標(biāo)，進而可表示過A，B兩點的直線方程
?設(shè)點：設(shè)出直線l與x軸交點，可表示出|DF|，進而表示出S△ABF，根據(jù)面積關(guān)系，可求得此點坐標(biāo)
?設(shè)點：要求此點的軌跡方程，先設(shè)出此點，根據(jù)題目條件得出此點坐標(biāo)的關(guān)系式，即軌跡方程
解決解析幾何問題的關(guān)鍵在于：通觀全局，局部入手，整體思維，反映在解題上，就是把曲線的幾何特征準確地轉(zhuǎn)換為代數(shù)形式，根據(jù)方程畫出圖形，研究幾何性質(zhì)．
2022年高考數(shù)學(xué)二輪復(fù)習(xí) 第1篇 專題7 解析幾何學(xué)案
