2022年六年級(jí)數(shù)學(xué)下冊(cè) 第七章 相交線與平行線單元綜合測(cè)試題 魯教版五四制

《2022年六年級(jí)數(shù)學(xué)下冊(cè) 第七章 相交線與平行線單元綜合測(cè)試題 魯教版五四制》由會(huì)員分享，可在線閱讀，更多相關(guān)《2022年六年級(jí)數(shù)學(xué)下冊(cè) 第七章 相交線與平行線單元綜合測(cè)試題 魯教版五四制（5頁珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

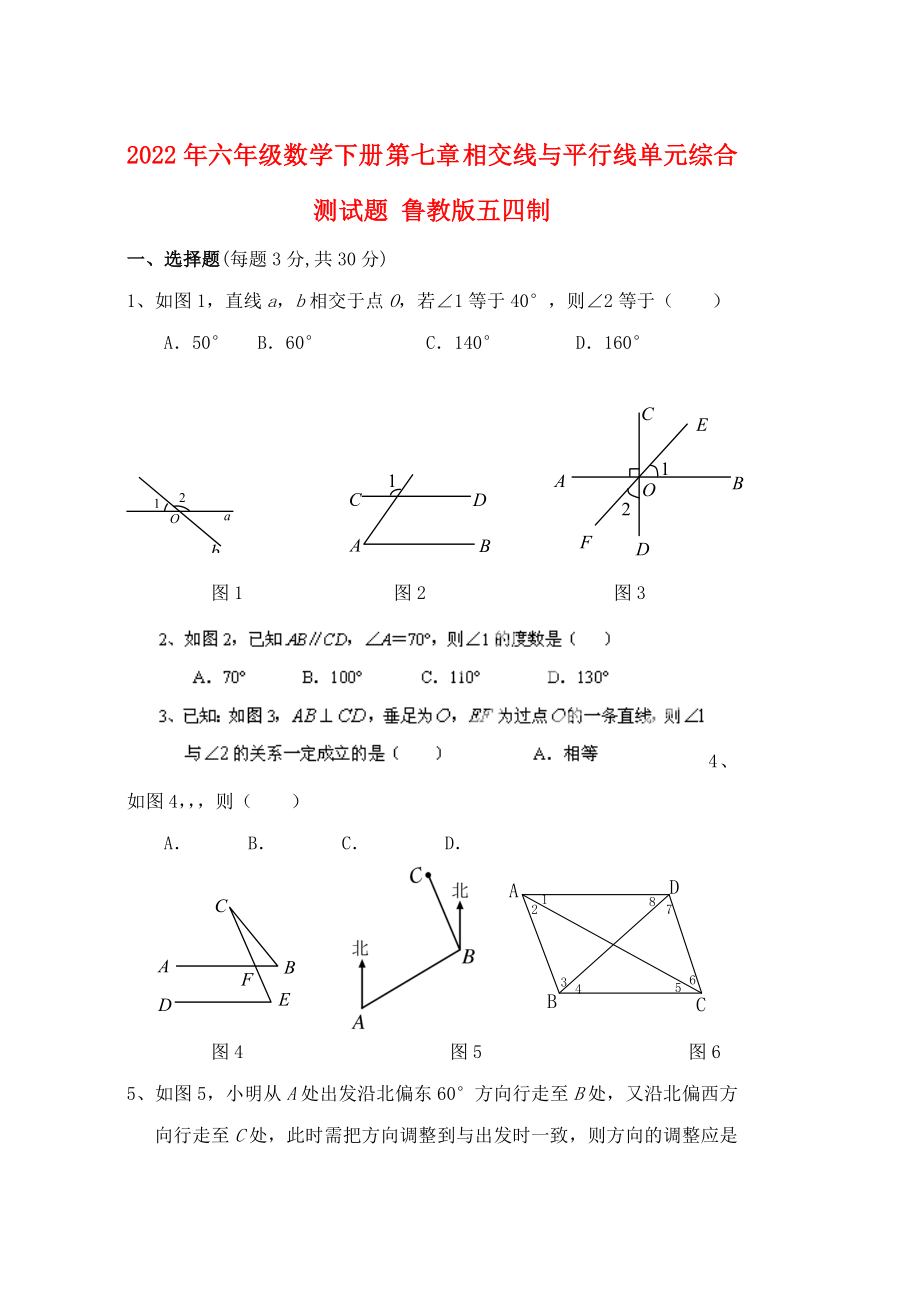
1、2022年六年級(jí)數(shù)學(xué)下冊(cè) 第七章 相交線與平行線單元綜合測(cè)試題 魯教版五四制 一、選擇題(每題3分,共30分) 1、如圖1，直線a，b相交于點(diǎn)O，若∠1等于40°，則∠2等于（ ） A．50° B．60° C．140° D．160° D B A C 1 a b 1 2 O A B C D E F 2 1 O 圖1 圖2 圖3 4、如圖4，，，則（ ） A． B． C． D．

2、B E D A C F 圖4 圖5 圖6 5、如圖5，小明從A處出發(fā)沿北偏東60°方向行走至B處，又沿北偏西方向行走至C處，此時(shí)需把方向調(diào)整到與出發(fā)時(shí)一致，則方向的調(diào)整應(yīng)是（ ） A．右轉(zhuǎn)80° B．左轉(zhuǎn)80° C．右轉(zhuǎn)100° D．左轉(zhuǎn)100° 6、如圖6，如果AB∥CD，那么下面說法錯(cuò)誤的是（ ） A．∠3=∠7； B．∠2=∠6 C、∠3+∠4+∠5+∠6=1800 D、∠4=

3、∠8 7、如果兩個(gè)角的兩邊分別平行，而其中一個(gè)角比另一個(gè)角的4倍少，那么這兩個(gè)角是（ ） A． B． 都是 C． 或 D． 以上都不對(duì) 8、下列語句：①三條直線只有兩個(gè)交點(diǎn)，則其中兩條直線互相平行；②如果兩條平行線被第三條截，同旁內(nèi)角相等，那么這兩條平行線都與第三條直線垂直；③過一點(diǎn)有且只有一條直線與已知直線平行，其中（ ） A．①、②是正確的命題；B．②、③是正確命題；C．①、③是正確命題 ；D．以上結(jié)論皆錯(cuò) 9、下列語句錯(cuò)誤的是（ ） A．連接兩點(diǎn)的線段的長(zhǎng)度叫做兩點(diǎn)間的距離；B．兩條直線平行，同旁內(nèi)角互補(bǔ) C．若兩個(gè)

4、角有公共頂點(diǎn)且有一條公共邊，和等于平角，則這兩個(gè)角為鄰補(bǔ)角 D．平移變換中，各組對(duì)應(yīng)點(diǎn)連成兩線段平行且相等 10、如圖7，，分別在上，為兩平行線間一點(diǎn)， 那么（ ） a b M P N 1 2 3 A． B． C． D． 圖7 二、填空題(每題4分,共24分) 11、如圖8，直線，直線與 相交．若，則． 1 2 b a c b a c d 1 2 3 4 A B C D E 圖8 圖9

5、 圖10 12、如圖9，已知?jiǎng)t______． 13、如圖10，已知AB∥CD，BE平分∠ABC，∠CDE＝150°，則∠C＝______ 14、如圖11，已知，，，則 ． CB A B D E A B C a b 1 2 3 圖11 圖12 圖13 15、如圖12所示，請(qǐng)寫出能判定CE∥AB的一個(gè)條件 ． 16、如圖13，已知

6、，=____________ 三、解答題 17、推理填空：(每空1分,共12分) 如圖： ① 若∠1=∠2，則 ∥ （ ） 若∠DAB+∠ABC=1800，則 ∥ （ ） ②當(dāng) ∥ 時(shí)，∠ C+∠ABC=1800（ ） 當(dāng) ∥ 時(shí)，∠3=∠C（ ） 18、如圖，∠1＝30°，AB⊥CD，垂足為O，EF經(jīng)過點(diǎn)O.求∠2、∠3的度數(shù). (8分) 19、已知：如圖AB∥CD

7、，EF交AB于G，交CD于F，F(xiàn)H平分∠EFD，交AB于H ，∠AGE=500，求：∠BHF的度數(shù)．(8分) 20、(10分)觀察如圖所示中的各圖，尋找對(duì)頂角（不含平角）： 圖a 圖b 圖c （1）如圖a，圖中共有＿＿＿對(duì)對(duì)頂角；（2）如圖b，圖中共有＿＿＿對(duì)對(duì)頂角； （3）如圖c，圖中共有＿＿＿對(duì)對(duì)頂角. （4）研究（1）～（3）小題中直線條數(shù)與對(duì)頂角的對(duì)數(shù)之間的關(guān)系，若有n條直線相交于一點(diǎn)， 則可形成多少對(duì)對(duì)頂角？ （5）若有xx條直線相交于一點(diǎn)，則可形成 多少對(duì)對(duì)頂角？ 21、(8分)已知，如圖，CD⊥AB，GF⊥AB，∠B＝∠ADE，試說明∠1＝∠2．