《高中數(shù)學(xué) 第一章 三角函數(shù) 1.1 任意角和弧度制 1.1.1 任意角學(xué)案 新人教A版必修4》由會員分享�,可在線閱讀,更多相關(guān)《高中數(shù)學(xué) 第一章 三角函數(shù) 1.1 任意角和弧度制 1.1.1 任意角學(xué)案 新人教A版必修4(8頁珍藏版)》請在裝配圖網(wǎng)上搜索�����。
1、
1.1.1 任意角
學(xué)習(xí)目標:1.理解任意角的概念.2.掌握終邊相同角的含義及其表示.(重點��、難點)3.掌握軸線角���、象限角及區(qū)間角的表示方法.(難點����、易錯點)
[自 主 預(yù) 習(xí)·探 新 知]
1.角的概念:角可以看成平面內(nèi)一條射線繞著端點從一個位置旋轉(zhuǎn)到另一個位置所形成的圖形.
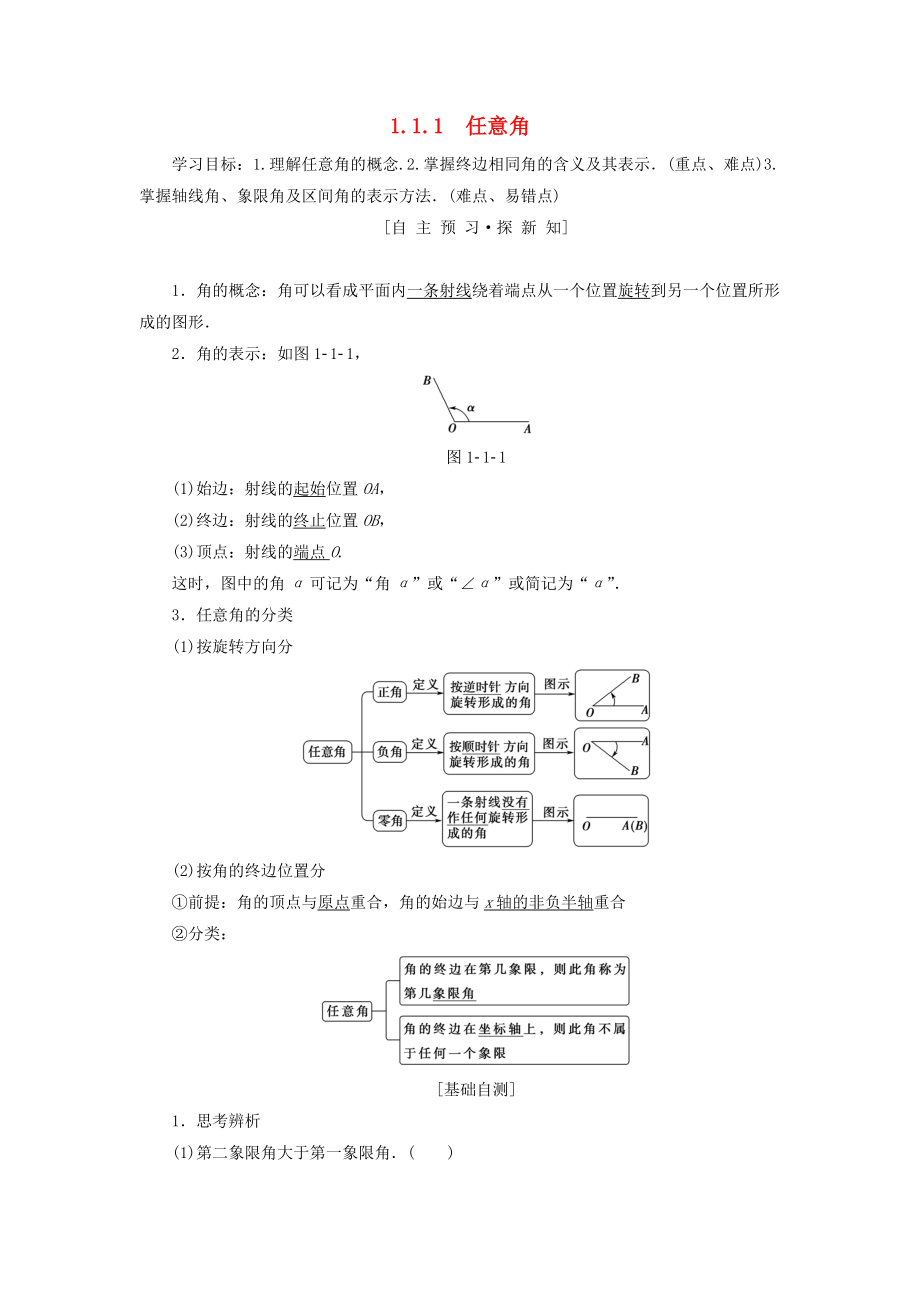
2.角的表示:如圖111��,
圖111
(1)始邊:射線的起始位置OA����,
(2)終邊:射線的終止位置OB,
(3)頂點:射線的端點O.
這時���,圖中的角α可記為“角α”或“∠α”或簡記為“α”.
3.任意角的分類
(1)按旋轉(zhuǎn)方向分
2��、
(2)按角的終邊位置分
①前提:角的頂點與原點重合�����,角的始邊與x軸的非負半軸重合
②分類:
[基礎(chǔ)自測]
1.思考辨析
(1)第二象限角大于第一象限角.( )
(2)第二象限角是鈍角.( )
(3)終邊相同的角不一定相等��,但相等的角終邊一定相同.( )
(4)終邊相同的角有無數(shù)個�,它們相差360°的整數(shù)倍.( )
[解析] (1)錯誤.如第二象限角100°小于第一象限角361°.
(2)錯誤.如第二象限角-181°不是鈍角.
(3)(4)都正確.
[答案] (1)× (2)× (3)√ (4
3���、)√
2.50°角的始邊與x軸的非負半軸重合��,把終邊按順時針方向旋轉(zhuǎn)2周����,所得角是________.
-670° [由題意知���,所得角是50°-2×360°=-670°.]
3.已知0°≤α<360°����,且α與600°角終邊相同����,則α=________,它是第________象限角.
240° 三 [因為600°=360°+240°��,所以240°角與600°角終邊相同����,且0°≤240°<360°,故α=240&#
4、176;���,它是第三象限角.]
[合 作 探 究·攻 重 難]
任意角和象限角的概念
(1)給出下列說法:
①銳角都是第一象限角�;②第一象限角一定不是負角��;③小于180°的角是鈍角�、直角或銳角;④始邊和終邊重合的角是零角.
其中正確說法的序號為________(把正確說法的序號都寫上).
(2)已知角的頂點與坐標原點重合�����,始邊與x軸的非負半軸重合����,作出下列各角,并指出它們是第幾象限角.
①420°.②855°.③-510°. 【導(dǎo)學(xué)號:84352000】
(1)① [(1)①銳角是大于0°且小于90°的
5�、角,終邊落在第一象限�,是第一象限角,所以①正確�;
②-350°角是第一象限角,但它是負角��,所以②錯誤�;
③0°角是小于180°的角����,但它既不是鈍角����,也不是直角或銳角�,所以③錯誤;
④360°角的始邊與終邊重合���,但它不是零角�,所以④錯誤.]
(2)作出各角的終邊��,如圖所示:
由圖可知:
①420°是第一象限角.
②855°是第二象限角.
③-510°是第三象限角.
[規(guī)律方法] 1.判斷角的概念問題的關(guān)鍵與技巧:
(1)關(guān)鍵:正確理解象限角與銳角���、直角���、鈍角、平角�、周角等概念.
(2)技巧:判斷命題為
6、真需要證明����,而判斷命題為假只要舉出反例即可.
2.象限角的判定方法:
(1)在坐標系中畫出相應(yīng)的角,觀察終邊的位置,確定象限.
(2)第一步�,將α寫成α=k·360°+β(k∈Z,0°≤β<360°)的形式;
第二步���,判斷β的終邊所在的象限��;
第三步��,根據(jù)β的終邊所在的象限�����,即可確定α的終邊所在的象限.
提醒:理解任意角這一概念時�����,要注意“旋轉(zhuǎn)方向”決定角的“正負”�,“旋轉(zhuǎn)幅度”決定角的“絕對值大小”.
[跟蹤訓(xùn)練]
1.已知集合A={第一象限角}�,B={銳角},C={小于90°的角}����,則下面關(guān)系正確的是( )
A.A
7、=B=C B.A?C
C.A∩C=B D.B∪C?C
D [由已知得BC�����,所以B∪C=C,故D正確.]
2.給出下列四個命題:①-75°是第四象限角��;②225°是第三象限角���;③475°是第二象限角���;④-315°是第一象限角.其中正確的命題有( )
【導(dǎo)學(xué)號:84352001】
A.1個 B.2個
C.3個 D.4個
D [-90°<-75°<0°���,180°<225°<270°�,
360°+90°<475°<360°+180�
8����、6;,-360°<-315°<-270°.所以這四個命題都是正確的.]
終邊相同的角的表示及應(yīng)用
(1)將-885°化為k·360°+α(0°≤α<360°��,k∈Z)的形式是________.
(2)寫出與α=-1 910°終邊相同的角的集合�����,并把集合中適合不等式-720°≤β<360°的元素β寫出來.
[思路探究] (1)根據(jù)-885°與k·360°����,k∈Z的關(guān)系確定k.
(2)先寫出與α終邊相同的角k·360°+α���,
9、k∈Z��,再由已知不等式確定k的可能取值.
(1)(-3)×360°+195° [(1)-885°=-1 080°+195°=(-3)×360°+195°.]
(2)與α=-1 910°終邊相同的角的集合為
{β|β=k·360°-1 910°�����,k∈Z}.
∵-720°≤β<360°����,即-720°≤k·360°-1 910°<360°(k∈Z),
∴3≤k<6(k∈Z)�����,故取k=4,5,6
10����、.
k=4時,β=4×360°-1 910°=-470°����;
k=5時����,β=5×360°-1 910°=-110°����;
k=6時,β=6×360°-1 910°=250°.
[規(guī)律方法] 1.在0°到360°范圍內(nèi)找與給定角終邊相同的角的方法
(1)一般地�����,可以將所給的角α化成k·360°+β的形式(其中0°≤β<360°���,k∈Z),其中的β就是所求的角.
(2)如果所給的角的絕對值不是很大�����,可以通過如下方法
11���、完成:當所給角是負角時��,采用連續(xù)加360°的方式��;當所給角是正角時����,采用連續(xù)減360°的方式,直到所得結(jié)果達到要求為止.
2.運用終邊相同的角的注意點
所有與角α終邊相同的角�,連同角α在內(nèi)可以用式子k·360°+α,k∈Z表示���,在運用時需注意以下四點:
(1)k是整數(shù)�,這個條件不能漏掉.
(2)α是任意角.
(3)k·360°與α之間用“+”連接�����,如k·360°-30°應(yīng)看成k·360°+(-30°)�,k∈Z.
(4)終邊相同的角不一定相等,但相等的角終邊一定相同
12����、,終邊相同的角有無數(shù)個��,它們相差周角的整數(shù)倍.
提醒:表示終邊相同的角�,k∈Z這一條件不能少.
[跟蹤訓(xùn)練]
3.下面與-850°12′終邊相同的角是( )
A.230°12′ B.229°48′
C.129°48′ D.130°12′
B [與-850°12′終邊相同的角可表示為α=-850°12′+k·360°(k∈Z),當k=3時�����,α=-850°12′+1 080°=229°48′.]
4.在-360°~360°之間找出所有與下列各角
13、終邊相同的角����,并判斷各角所在的象限.
①790°;②-20°. 【導(dǎo)學(xué)號:84352002】
[解]?����、佟?90°=2×360°+70°=3×360°-290°����,
∴在-360°~360°之間與它終邊相同的角是70°和-290°,它們都是第一象限的角.
②∵-20°=-360°+340°�����,
∴在-360°~360°之間與它終邊相同的角是-20°和340°�����,它們都是第四象限的角.
14����、任意角終邊位置的確定和表示
[探究問題]
1.若射線OA的位置是k·360°+10°�,k∈Z��,射線OA繞點O逆時針旋轉(zhuǎn)90°經(jīng)過的區(qū)域為D���,則終邊落在區(qū)域D(包括邊界)的角的集合應(yīng)如何表示?
提示:終邊落在區(qū)域D包括邊界的角的集合可表示為{α|k·360°+10°≤α≤k·360°+100°��,k∈Z}.
2.若角α與β的終邊關(guān)于x軸���、y軸����、原點�����、直線y=x對稱���,則角α與β分別具有怎樣的關(guān)系����?
[提示] (1)關(guān)于x軸對稱:若角α與β的終邊關(guān)于x軸對稱���,則角α與β的關(guān)系是β=-α+k&#
15��、183;360°�,k∈Z.
(2)關(guān)于y軸對稱:若角α與β的終邊關(guān)于y軸對稱,則角α與β的關(guān)系是β=180°-α+k·360°��,k∈Z.
(3)關(guān)于原點對稱:若角α與β的終邊關(guān)于原點對稱��,則角α與β的關(guān)系是β=180°+α+k·360°�,k∈Z.
(4)關(guān)于直線y=x對稱:若角α與β的終邊關(guān)于直線y=x對稱,則角α與β的關(guān)系是β=-α+90°+k·360°�����,k∈Z.
(1)若α是第一象限角���,則-是( )
A.第一象限角 B.第一�、四象限角
C.第二象限角 D.第二��、四象限角
16���、
(2)已知,如圖112所示.
圖112
①分別寫出終邊落在OA��,OB位置上的角的集合.
②寫出終邊落在陰影部分(包括邊界)的角的集合.
[思路探究] (1)→→
(2)①→
②
→
(1)D [(1)因為α是第一象限角,所以k·360°<α<k·360°+90°���,k∈Z��,
所以k·180°<<k·180°+90°�,k∈Z����,
所以是第一、三象限角���,
又因為-與的終邊關(guān)于x軸對稱����,
所以-是第二�、四象限角.]
(
17、2)①終邊落在OA位置上的角的集合為{α|α=90°+45°+k·360°�,k∈Z}={α|α=135°+k·360°,k∈Z}����;
終邊落在OB位置上的角的集合為{α|α=-30°+k·360°,k∈Z}.
②由題干圖可知���,陰影部分(包括邊界)的角的集合是由所有介于[-30°�����,135°]之間的與之終邊相同的角組成的集合�,故該區(qū)域可表示為{α|-30°+k·360°≤α≤135°+k·360°,k∈Z}.
母題探
18����、究:1.若將本例(2)改為如圖113所示的圖形,那么終邊落在陰影部分(包括邊界)的角的集合如何表示���?
圖113
[解] 在0°~360°范圍內(nèi)����,終邊落在陰影部分(包括邊界)的角為60°≤β<105°與240°≤β<285°��,所以所有滿足題意的角β為{β|k·360°+60°≤β<k·360°+105°��,k∈Z}∪{β|k·360°+240°≤β<k·360°+285�
19��、76;��,k∈Z}
={β|2k·180°+60°≤β<2k·180°+105°���,k∈Z}∪{β|(2k+1)·180°+60°≤β<(2k+1)·180°+105°����,k∈Z}
={β|n·180°+60°≤β<n·180°+105°�����,n∈Z}.
故角β的取值集合為{β|n·180°+60°≤β<n·180°+105°�����,n∈Z}.
2.若將本例(2)改
20����、為如圖114所示的圖形,那么陰影部分(包括邊界)表示的終邊相同的角的集合如何表示��?
圖114
[解] 在0°~360°范圍內(nèi)����,陰影部分(包括邊界)表示的范圍可表示為:150°≤β≤225°,則所有滿足條件的角β為{β|k·360°+150°≤β≤k·360°+225°����,k∈Z}.
[規(guī)律方法] 1.表示區(qū)間角的三個步驟:
第一步:先按逆時針的方向找到區(qū)域的起始和終止邊界���;
第二步:按由小到大分別標出起始和終止邊界對應(yīng)的-360�
21、6;~360°范圍內(nèi)的角α和β�,寫出最簡區(qū)間{x|α<x<β},其中β-α<360°����;
第三步:起始、終止邊界對應(yīng)角α����,β再加上360°的整數(shù)倍,即得區(qū)間角集合.
2.nα或所在象限的判斷方法:
(1)用不等式表示出角nα或的范圍��;
(2)用旋轉(zhuǎn)的觀點確定角nα或所在象限.
例如:k·120°<<k·120°+30°�,k∈Z.
由0°<<30°,每次逆時針旋轉(zhuǎn)120°可得終邊的位置.
提醒:表示區(qū)間角時要注意實線邊界與虛線邊界的差異.
[當 堂 達 標
22����、·固 雙 基]
1.下列說法正確的是( )
A.三角形的內(nèi)角是第一象限角或第二象限角
B.第四象限的角一定是負角
C.60°角與600°角是終邊相同的角
D.將表的分針撥慢10分鐘,則分針轉(zhuǎn)過的角為60°
D [A錯誤���,90°角既不是第一象限角也不是第二象限角���;
B錯誤��,280°角是第四象限角�����,但它不是負角;
C錯誤�����,600°-60°=540°不是360°的倍數(shù)�;
D正確,分針轉(zhuǎn)一周為60分鐘����,轉(zhuǎn)過的角度為-360°,將分針撥慢是逆時針旋轉(zhuǎn)�����,撥慢10分鐘轉(zhuǎn)過的角為3
23����、60°×=60°.]
2.下列各個角中與2 017°終邊相同的是( )
A.-147° B.677°
C.317° D.217°
D [因為2 017°=360°×5+217°,所以與2 017°終邊相同的角是217°.]
3.已知角α的終邊在如圖115陰影表示的范圍內(nèi)(不包含邊界)�,那么角α的集合是________. 【導(dǎo)學(xué)號:84352004】
圖115
{α|k&
24���、#183;360°+45°<α<k·360°+150°,k∈Z} [觀察圖形可知�,角α的集合是{α|k·360°+45°<α<k·360°+150°,k∈Z}.]
4.角α���,β的終邊關(guān)于y軸對稱�����,若α=30°��,則β=________.
150°+k·360°�,k∈Z [∵30°與150°的終邊關(guān)于y軸對稱�����,
∴β的終邊與150°角的終邊相同.
∴β=150°+k·360°�����,k∈Z
25�、.]
5.在0°到360°范圍內(nèi),找出與下列各角終邊相同的角,并判斷它們是第幾象限的角:
(1)-120°���;(2)640°.
【導(dǎo)學(xué)號:84352005】
[解] (1)與-120°終邊相同的角的集合為M={β|β=-120°+k·360°���,k∈Z}.
當k=1時,β=-120°+1×360°=240°�,
∴在0°到360°范圍內(nèi),與-120°終邊相同的角是240°�����,它是第三象限的角.
(2)與640°終邊相同的角的集合為M={β|β=640°+k·360°����,k∈Z}.
當k=-1時��,β=640°-360°=280°�����,
∴在0°到360°范圍內(nèi)��,與640°終邊相同的角為280°����,它是第四象限的角.
我國經(jīng)濟發(fā)展進入新常態(tài)��,需要轉(zhuǎn)變經(jīng)濟發(fā)展方式����,改變粗放式增長模式���,不斷優(yōu)化經(jīng)濟結(jié)構(gòu)���,實現(xiàn)經(jīng)濟健康可持續(xù)發(fā)展進區(qū)域協(xié)調(diào)發(fā)展,推進新型城鎮(zhèn)化�,推動城鄉(xiāng)發(fā)展一體化因:我國經(jīng)濟發(fā)展還面臨區(qū)域發(fā)展不平衡、城鎮(zhèn)化水平不高�、城鄉(xiāng)發(fā)展不平衡不協(xié)調(diào)等現(xiàn)實挑戰(zhàn)。
 高中數(shù)學(xué) 第一章 三角函數(shù) 1.1 任意角和弧度制 1.1.1 任意角學(xué)案 新人教A版必修4
高中數(shù)學(xué) 第一章 三角函數(shù) 1.1 任意角和弧度制 1.1.1 任意角學(xué)案 新人教A版必修4