《17.1 勾股定理 教學(xué)設(shè)計 --2023--2024學(xué)年人教版八年級數(shù)學(xué)下冊》由會員分享，可在線閱讀，更多相關(guān)《17.1 勾股定理 教學(xué)設(shè)計 --2023--2024學(xué)年人教版八年級數(shù)學(xué)下冊（6頁珍藏版）》請在裝配圖網(wǎng)上搜索。
1、第十七章 勾股定理
17.1 勾股定理
第1課時 勾股定理
學(xué)習(xí)目標(biāo)：1.經(jīng)歷勾股定理的探究過程，了解關(guān)于勾股定理的一些文化歷史背景，會用
面積法來證明勾股定理，體會數(shù)形結(jié)合的思想；
2.會用勾股定理進(jìn)行簡單的計算.
重點：用面積法來證明勾股定理，體會數(shù)形結(jié)合的思想.
難點：會用勾股定理進(jìn)行簡單的計算.
教學(xué)過程
一、 要點探究
勾股定理的認(rèn)識及驗證
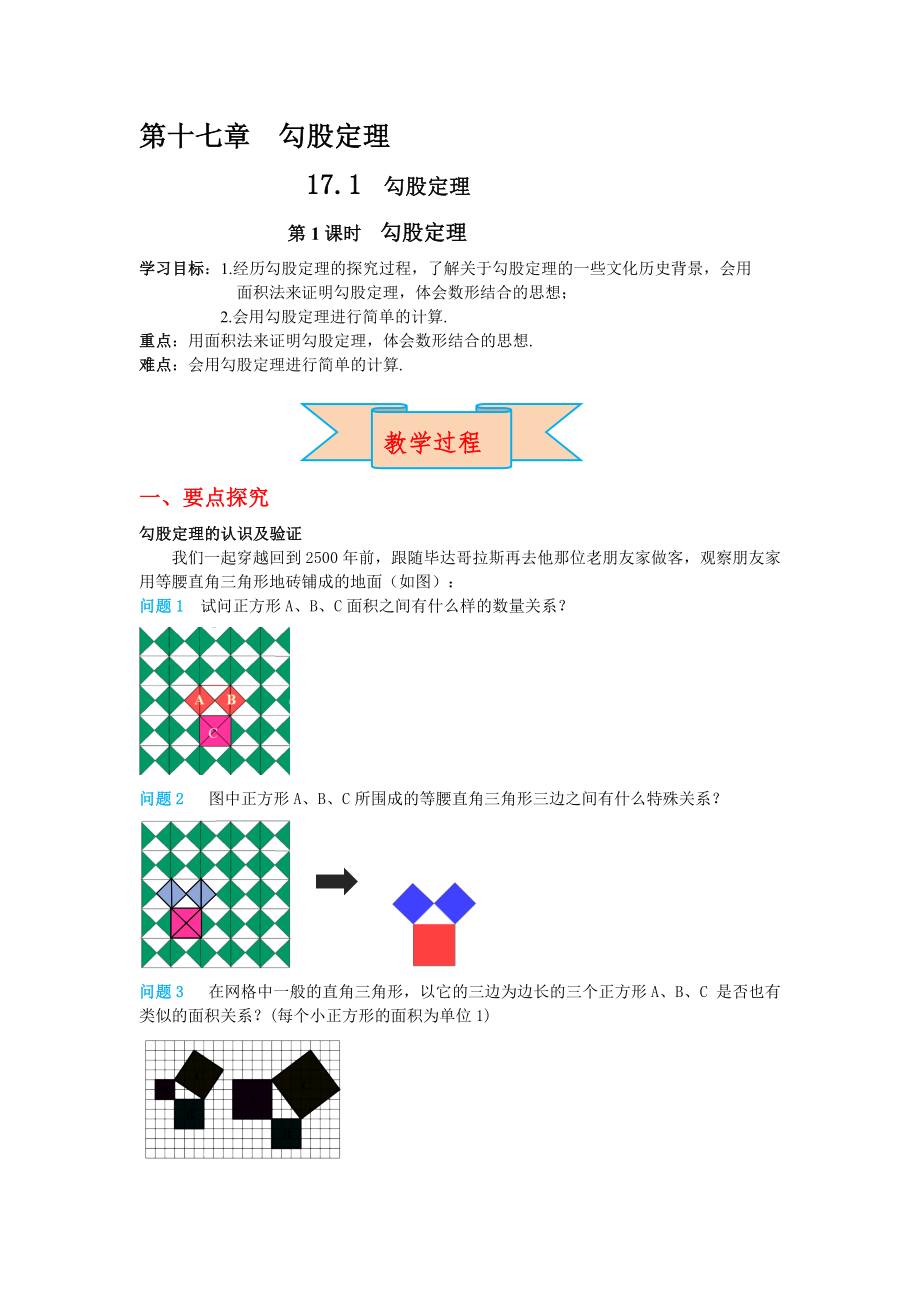
我們一起穿越回到2500年前，跟隨畢達(dá)哥拉斯再去他那位老朋友家做客，觀察朋友家用等腰直角三角形地磚鋪成的地面（如圖）：
問題1 試問正方形A、B、C面積之間有什么樣的數(shù)量關(guān)系？
問題2
2、 圖中正方形A、B、C所圍成的等腰直角三角形三邊之間有什么特殊關(guān)系？
A
問題3 在網(wǎng)格中一般的直角三角形，以它的三邊為邊長的三個正方形A、B、C 是否也有類似的面積關(guān)系？(每個小正方形的面積為單位1)
思考：這兩幅圖中A,B的面積都好求，該怎樣求C的面積呢？
方法1：補(bǔ)形法(把以斜邊為邊長的正方形補(bǔ)成各邊都在網(wǎng)格線上的正方形）：
左圖：
右圖：
方法2：分割法(把以斜邊為邊長的正方形分割成易求出面積的三角形和四邊形）：
根據(jù)前面求出的C的面積直接填出下表：
3、思考 正方形A、B、C 所圍成的直角三角形三條邊之間有怎樣的特殊關(guān)系？
你能結(jié)合字母表示出來嗎？
命題：如果直角三角形的兩條直角邊長分別為a,b，斜邊長為c,那么a2 + b2 = c2。
二、小組活動
以小組為單位，剪4個完全相同的直角三角形，類比探究思考中求解正方形C的面積方法，拼一拼，擺一擺，看看能否得到一個正方形，并利用等面積法證明勾股定理.
借助數(shù)字教材中的拼圖，學(xué)生上臺展示。
活動2
證法1 讓我們跟著我國漢代數(shù)學(xué)家趙爽拼圖,再用所拼的圖形證明命題吧.
趙爽弦圖”表現(xiàn)了我國古人對數(shù)學(xué)的鉆研精神和
4、聰明才智，它是我國古代數(shù)學(xué)的驕傲.因此，這個圖案被選為2002年在北京召開的國際數(shù)學(xué)大會的會徽.
證法2 畢達(dá)哥拉斯證法，請先用手中的四個全等的直角三角形按圖示進(jìn)行拼圖，然后分析其面積關(guān)系后證明吧.
證明：
∵S大正方形=(a+b)2=a2+b2+2ab,
S大正方形=4S直角三角形+ S小正方形=
∴a2+b2+2ab=c2+2ab，
∴a2 +b2 =c2.
證法3 美國第二十任總統(tǒng)加菲爾德的“總統(tǒng)證法”.
如圖，圖中的三個三角形都是直角三角形，求證：a2 + b2 = c2.
三、歸納總結(jié)
勾股定理：如果直角三角形的兩直角邊長分別為a
5、,b,斜邊長為c,那么a2+b2=c2.
公式變形：
小貼士：在中國古代，人們把彎曲成直角的手臂的上半部分稱為“勾”，下半部分稱為“股”.我國古代學(xué)者把直角三角形較短的直角邊稱為“勾”，較長的直角邊稱為“股”，斜邊稱為“弦”.
四、利用勾股定理進(jìn)行計算
游戲競賽環(huán)節(jié)：兩名學(xué)生上臺進(jìn)行游戲競賽。
五、典例精析
例1如圖，在Rt△ABC中， ∠C=90°.
（1） 若a=b=5,求c;
（2） 若a=1,c=2,求b.
例2 已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的長.
方法總結(jié):由直角三角形的面積求法可知直角三角形兩直角邊的積
6、等于斜邊與斜邊上高的
積，它常與勾股定理聯(lián)合使用．
變式題2 在Rt△ABC中，AB＝4，AC＝3，求BC的長.
方法總結(jié):當(dāng)直角三角形中所給的兩條邊沒有指明是斜邊或直角邊時，其中一較長邊可能是
直角邊，也可能是斜邊，這種情況下一定要進(jìn)行分類討論，否則容易丟解.
六、當(dāng)堂檢測
1. 求下列圖中未知數(shù)x、y的值：
2.下列說法中,正確的是（ ）
A.已知a,b,c是三角形的三邊，則a2+b2=c2
B.在直角三角形中兩邊和的平方等于第三邊的平方
C.在Rt△ABC中，∠C=90°,所以a2+b2=c2
D.在Rt△
7、ABC中，∠B=90°,所以a2+b2=c2
3.圖中陰影部分是一個正方形，則此正方形的面積為_____________.
4.在△ABC中，∠C=90°.
（1）若a=15，b=8，則c=_______.
（2）若c=13，b=12，則a=_______.
5.若直角三角形中，有兩邊長是5和7，則第三邊長的平方為_________.
6.如圖，在△ABC中，AD⊥BC，∠B=45°，∠C=30°，AD=1，求△ABC的周長．
七、課堂小結(jié)
八、布置作業(yè)
必做題：登錄國家智慧中小學(xué)平臺進(jìn)入17.1勾股定理習(xí)題庫進(jìn)行檢測。
活動探究：課本36頁數(shù)學(xué)活動二，借助數(shù)字教材進(jìn)行活動探究。
17.1 勾股定理 教學(xué)設(shè)計 --2023--2024學(xué)年人教版八年級數(shù)學(xué)下冊
