《九年級數(shù)學(xué)上冊 第二章 對稱圖形-圓 第20講 圓周角的應(yīng)用課后練習(xí) （新版）蘇科版》由會員分享，可在線閱讀，更多相關(guān)《九年級數(shù)學(xué)上冊 第二章 對稱圖形-圓 第20講 圓周角的應(yīng)用課后練習(xí) （新版）蘇科版（3頁珍藏版）》請在裝配圖網(wǎng)上搜索。
1、九年級數(shù)學(xué)上冊 第二章 對稱圖形-圓 第20講 圓周角的應(yīng)用課后練習(xí) （新版）蘇科版
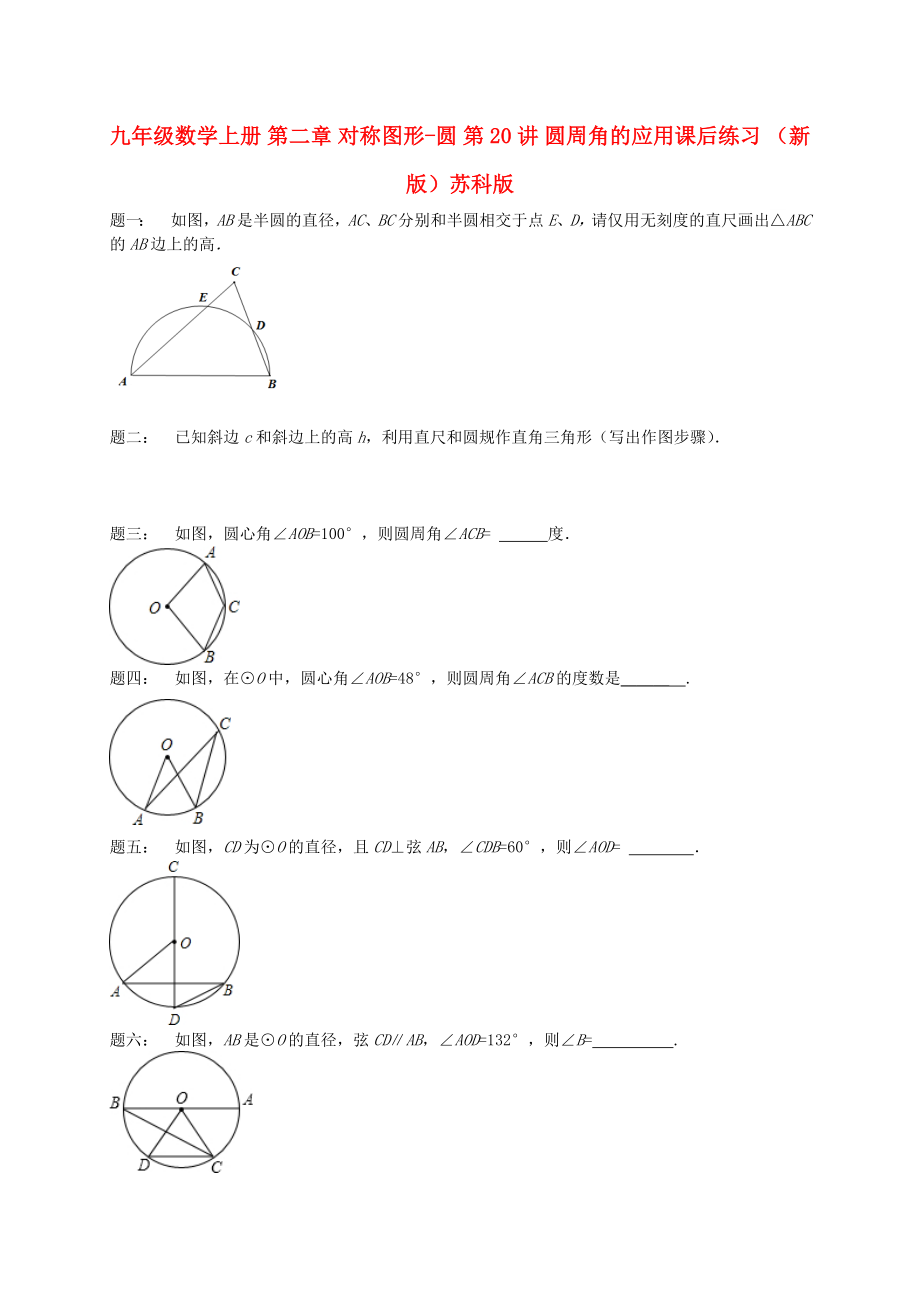
題一： 如圖，AB是半圓的直徑，AC、BC分別和半圓相交于點E、D，請僅用無刻度的直尺畫出△ABC的AB邊上的高．
題二： 已知斜邊c和斜邊上的高h(yuǎn)，利用直尺和圓規(guī)作直角三角形（寫出作圖步驟）．
題三： 如圖，圓心角∠AOB=100°，則圓周角∠ACB= 130 度．
題四： 如圖，在⊙O中，圓心角∠AOB=48°，則圓周角∠ACB的度數(shù)是______ .
題五： 如圖，CD為⊙O的直徑，且CD⊥弦AB，∠CDB=60°，則∠AOD= 60 ．
2、
題六： 如圖，AB是⊙O的直徑，弦CD∥AB，∠AOD=132°，則∠B= .
第20講 圓周角的應(yīng)用
題一： 見詳解．
詳解：如圖所示：
①連接AD、BE，因為AB是半圓的直徑，所以∠AEB=∠ADB=90°，所以AD、BE分別是邊BC和AC上的高，
②設(shè)AD、BE相交于點M，連接CM并延長交AB于點H，
③CH即為所求的△ABC的AB邊上的高 (根據(jù)三角形的三條高線交于一點)．
題二： 見詳解．
詳解：如圖所示：
①作射線AD，在射線上截取AB=c，
②以AB為直徑作半圓，
③作AB的平行線l，使兩平行線相距h，
④直線l與半圓的
3、交點即為直角三角形的頂點C，
⑤連接BC、AC，△ABC即為所求的直角三角形．
題三： 130.
詳解：在優(yōu)弧AB上取點D（不與A、B重合），連接AD、BD；
則∠ADB=∠AOB=×100°=50°；
∵四邊形ADBC內(nèi)接于⊙O，
∴∠ACB=180°-∠ADB=180°-50°=130°
題四： 24°．
詳解：根據(jù)一條弧所對的圓周角等于它所對的圓心角的一半，得∠ACB=∠AOB=24°．
題五： 60°．
詳解：∵ CD⊥弦AB，且∠CDB=60°，
∴∠B=180°-90°-60°=30°，
∵CD為⊙O的直徑，∠AOD為圓心角，
題六： ∵∠AOD=132°，∴∠BOD=48°，
∴∠BCD=∠BOD=24°，
∵CD∥AB，
∴∠B=∠BCD=24°．
九年級數(shù)學(xué)上冊 第二章 對稱圖形-圓 第20講 圓周角的應(yīng)用課后練習(xí) （新版）蘇科版
