《2022年高中數(shù)學(xué) 不等式的實際應(yīng)用學(xué)案 新人教B版必修5高二》由會員分享�����,可在線閱讀��,更多相關(guān)《2022年高中數(shù)學(xué) 不等式的實際應(yīng)用學(xué)案 新人教B版必修5高二(2頁珍藏版)》請在裝配圖網(wǎng)上搜索���。
1���、高二數(shù)學(xué) 必修五 NO 17 使用時間:
班級: 組別:
2022年高中數(shù)學(xué) 不等式的實際應(yīng)用學(xué)案 新人教B版必修5高二
學(xué)習(xí)目標(biāo)
1、通過實際問題的情景�,讓學(xué)生掌握不等式的實際應(yīng)用,掌握解決這類問題的一般步驟����,
2、讓學(xué)生經(jīng)歷從實際情景中抽象出不等式模型的過程�。
3、通過實例��,讓學(xué)生體驗數(shù)學(xué)與日常生活的聯(lián)系,感受數(shù)學(xué)的實用價值���,增強(qiáng)學(xué)生的應(yīng)用意識���,提高他們的實踐能力。
自主學(xué)習(xí)
1�����、比較兩實數(shù)大小的常用方法
2���、
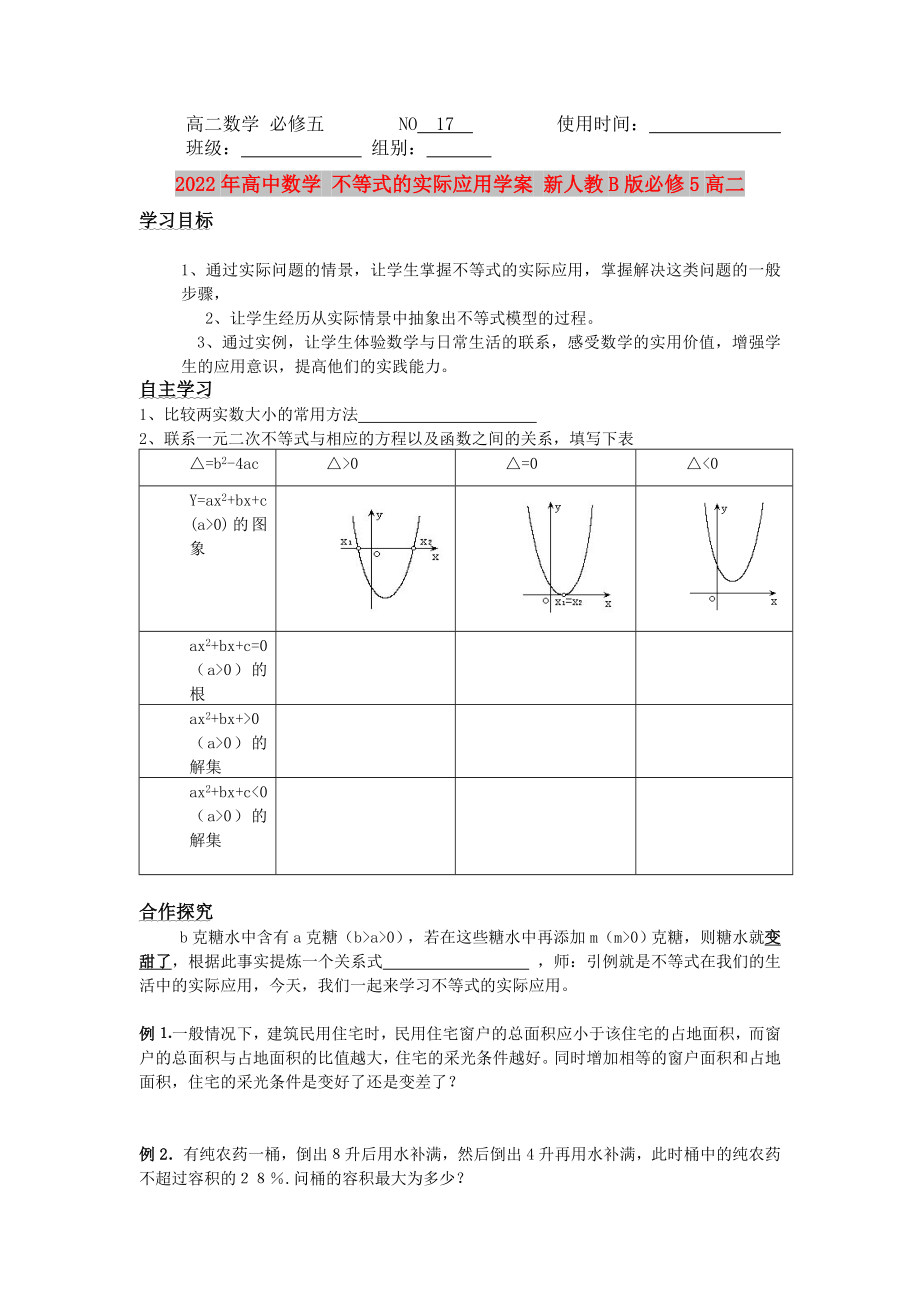
2�、聯(lián)系一元二次不等式與相應(yīng)的方程以及函數(shù)之間的關(guān)系���,填寫下表
△=b2-4ac
△>0
△=0
△<0
Y=ax2+bx+c
(a>0)的圖象
ax2+bx+c=0
(a>0)的根
ax2+bx+>0
(a>0)的解集
ax2+bx+c<0
(a>0)的解集
合作探究
b克糖水中含有a克糖(b>a>0)�,若在這些糖水中再添加m(m>0)克糖����,則糖水就變甜了,根據(jù)此事實提煉一個關(guān)系式 �����,師:引例就是不
3��、等式在我們的生活中的實際應(yīng)用��,今天����,我們一起來學(xué)習(xí)不等式的實際應(yīng)用。
例⒈一般情況下���,建筑民用住宅時�����,民用住宅窗戶的總面積應(yīng)小于該住宅的占地面積��,而窗戶的總面積與占地面積的比值越大��,住宅的采光條件越好�。同時增加相等的窗戶面積和占地面積����,住宅的采光條件是變好了還是變差了?
例2.有純農(nóng)藥一桶��,倒出8升后用水補(bǔ)滿,然后倒出4升再用水補(bǔ)滿���,此時桶中的純農(nóng)藥不超過容積的28%.問桶的容積最大為多少�����?
分析:若桶的容積為x, 倒前純農(nóng)藥為x升
第一次 :倒出純農(nóng)藥8升����,純農(nóng)藥還剩(x-8)升���,桶內(nèi)溶液濃度
第二次 :倒出溶液4升���,純農(nóng)藥還剩[(x-8)—()4],
中本題的不等關(guān)
4��、系是:桶中的農(nóng)藥不超過容積的28%
解答:學(xué)生完成�����。
例3.解在章頭語中提出的有關(guān)恩格爾系數(shù)的應(yīng)用問題:
根據(jù)某鄉(xiāng)鎮(zhèn)家庭抽樣調(diào)查的統(tǒng)計��,xx年每戶家庭年平均消費支出總額為1萬元�����,其中食品消費額為0.6萬元。預(yù)測xx年后��,每戶家庭年平均消費支出總額每年增加3000元�,如果到xx年該鄉(xiāng)鎮(zhèn)居民生活狀況能達(dá)到小康水平(即恩格爾系數(shù)n滿足條件(40﹪<n<50% ),試問這個鄉(xiāng)鎮(zhèn)每戶食品消費額平均每年的增長率至多是多少(精確到0.1)�。注:恩格爾系數(shù)n的計算公式是
鞏固檢測與課時作業(yè)
1、某出版社�,如果以每本2.50元的價格發(fā)行一種圖書,可發(fā)行80 000本�����。如果一本書的定價每升高0.1元��,發(fā)行量就減少xx本�����,那么要使收入不低于200 000元��,這種書的最高定價應(yīng)當(dāng)是多少�����?
2、某工人共加工300個零件��。在加工100個零件后����,改進(jìn)了操作方法,每天多加工15個���,用了不到20天的時間就完成了任務(wù)����。問改進(jìn)操作方法前��,每天至少要加工多少個零件��?
3����、教材83頁
 2022年高中數(shù)學(xué) 不等式的實際應(yīng)用學(xué)案 新人教B版必修5高二
2022年高中數(shù)學(xué) 不等式的實際應(yīng)用學(xué)案 新人教B版必修5高二