《2022年高二數(shù)學(xué)上學(xué)期第一次月考試題 文(無答案)(I)》由會員分享����,可在線閱讀,更多相關(guān)《2022年高二數(shù)學(xué)上學(xué)期第一次月考試題 文(無答案)(I)(3頁珍藏版)》請?jiān)谘b配圖網(wǎng)上搜索�。
1、2022年高二數(shù)學(xué)上學(xué)期第一次月考試題 文(無答案)(I)
一�����、選擇題:本大題共12小題��,每小題5分����,共60分.在每小題給出的四個選項(xiàng)中,只有一項(xiàng)是符合題目要求的.
1. 已知集合��,�,則( )
(A) (B) (C) (D)
2.在等差數(shù)列中,���,�����,則=
(A)5 (B)8 (C)10 (D)14
3. 為了調(diào)查城市PM2.5的情況���,按地域把48個城市分成大型���、中型、小型三組���,相應(yīng)的城市數(shù)分別為8���,16,24.若用分層抽樣的方法抽取12個城市�,則應(yīng)抽取的中型城市數(shù)為( )
(A)3 (B)4 (C)5
2、 (D)6
4. 設(shè),且��,則下列不等式成立的是 ( )
(A) (B) (C) (D)
5. 要得到函數(shù)的圖象��,只需將函數(shù)的圖象( )
(A)向左平移個單位 (B)向右平移個單位
(C)向左平移個單位 (D)向右平移個單位
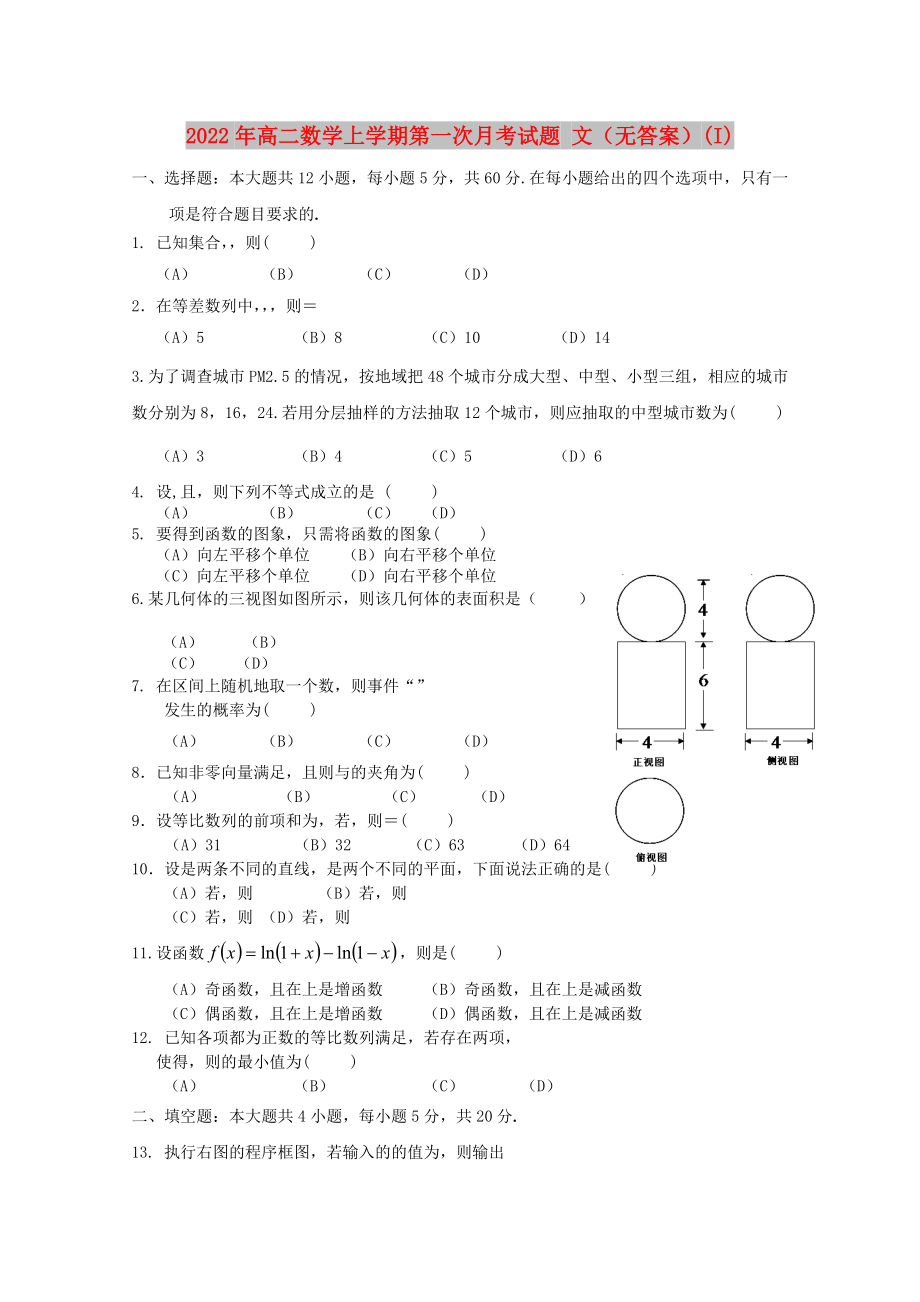
6.某幾何體的三視圖如圖所示��,則該幾何體的表面積是( )
(A) (B)
(C) (D)
7. 在區(qū)間上隨機(jī)地取一個數(shù)����,則事件“”
發(fā)生的概率為( )
(A) (B) (C) (D)
8.已知非零向量滿足����,且則與的夾角為( )
(A)
3�、(B) (C) (D)
9.設(shè)等比數(shù)列的前項(xiàng)和為,若��,則=( )
(A)31 (B)32 (C)63 (D)64
10.設(shè)是兩條不同的直線��,是兩個不同的平面�,下面說法正確的是( )
(A)若����,則 (B)若,則
(C)若���,則 (D)若����,則
11.設(shè)函數(shù)���,則是( )
(A)奇函數(shù)����,且在上是增函數(shù) (B)奇函數(shù),且在上是減函數(shù)
(C)偶函數(shù)�����,且在上是增函數(shù) (D)偶函數(shù)�,且在上是減函數(shù)
12. 已知各項(xiàng)都為正數(shù)的等比數(shù)列滿足,若存在兩項(xiàng)����,
使得,則的最小值為(
4���、 )
(A) (B) (C) (D)
二��、填空題:本大題共4小題�,每小題5分�,共20分.
13. 執(zhí)行右圖的程序框圖,若輸入的的值為����,則輸出
的的值是 .
14. 若,滿足約束條件則的
最大值為 .
15. 的內(nèi)角的對邊分別為���,
已知����,則的面積為
16. 已知函數(shù)(其中是自然對數(shù)的底數(shù)),若關(guān)于的不等式在上恒成立�����,則實(shí)數(shù)的取值范圍是 .
三�����、解答題:本大題共6小題����,共70分.
17.(本小題滿分10分)
如圖,在直三棱柱中, ,點(diǎn)是的中點(diǎn).
(I)求證:
(II)求證:
5����、平面
18.(本小題滿分12分)
某中學(xué)調(diào)查了某班全部名同學(xué)參加書法社團(tuán)和演講社團(tuán)的情況,數(shù)據(jù)如下表:(單位:人)
參加書法社團(tuán)
未參加書法社團(tuán)
參加演講社團(tuán)
未參加演講社團(tuán)
(I)從該班隨機(jī)選名同學(xué)���,求該同學(xué)至少參加上述一個社團(tuán)的概率�����;
(II)在既參加書法社團(tuán)又參加演講社團(tuán)的名同學(xué)中���,有名男同學(xué)名女同學(xué). 現(xiàn)從這名男同學(xué)和名女同學(xué)中各隨機(jī)選人����,求被選中且未被選中的概率.
18�����、(本題滿分12分)
袋中裝有3個紅球和2個黑球�����,一次取3個球�����。
(I)求取出的3個球中恰有2個紅球的概率��;
(II)取出的3個球中�,紅球數(shù)多于黑球數(shù)的概率。
6�、
19.(本小題滿分12分)
已知函數(shù),.
(I)求函數(shù)的最小值和最小正周期���;
(II)已知內(nèi)角�����、���、的對邊分別為����、���、���,且����,,���,求�����、的值.
20. (本小題滿分12分)
如圖所示�,在四棱錐中,底面為矩形��,
平面��,點(diǎn)在線段上��,平面.
(I)證明:平面��;
(II)若��,�����,求點(diǎn)到平面的距離.
21.(本小題滿分12分)
已知等差數(shù)列的前項(xiàng)和為��,等比數(shù)列中首項(xiàng)公比 ���,且是和的等差中項(xiàng)�。
(I)求數(shù)列的通項(xiàng)公式����;
(II)設(shè)����,求數(shù)列的前項(xiàng)和.
22.(本小題滿分12分)
如圖所示��,四棱錐的底面是邊長為的正方形���,四條側(cè)棱長均為�,點(diǎn)分別是棱上共面的四點(diǎn)�,平面⊥平面,.
(I)證明:�;
(II)若,求四棱錐的體積.
 2022年高二數(shù)學(xué)上學(xué)期第一次月考試題 文(無答案)(I)
2022年高二數(shù)學(xué)上學(xué)期第一次月考試題 文(無答案)(I)